题目内容
已知抛物线y=
x2-
x-1.
(1)求它的顶点M的坐标;
(2)求它与x轴的两个交点A、B(A左B右)的坐标,并画出草图;
(3)观察草图指出,当x为何值时,y=0?y<0?y>0?
(4)设抛物线与y轴的交点为C,求四边形ABMC的面积.
| 1 |
| 3 |
| 2 |
| 3 |
(1)求它的顶点M的坐标;
(2)求它与x轴的两个交点A、B(A左B右)的坐标,并画出草图;
(3)观察草图指出,当x为何值时,y=0?y<0?y>0?
(4)设抛物线与y轴的交点为C,求四边形ABMC的面积.
考点:抛物线与x轴的交点,二次函数图象上点的坐标特征,二次函数与不等式(组)
专题:
分析:(1)把抛物线方程转化为顶点式方程,然后可以直接写出答案;
(2)根据抛物线方程求得点A、B的坐标,然后由抛物线开口方程、顶点坐标、与y轴的交点以及顶点坐标画出草图;
(3)根据图形写出答案;
(4)将四边形ABMC分成梯形和两个直角三角形三部分来求.
(2)根据抛物线方程求得点A、B的坐标,然后由抛物线开口方程、顶点坐标、与y轴的交点以及顶点坐标画出草图;
(3)根据图形写出答案;
(4)将四边形ABMC分成梯形和两个直角三角形三部分来求.
解答:解:(1)∵y=
x2-
x-1=
(x-1)2-
,
∴它的顶点M的坐标为:(1,-
).
(2)令y=0,则
x2-
x-1=0,
整理,得
(x-3)(x+1)=0,
解得 x1=3,x2=-1,
∵该抛物线与x轴的两个交点A在B的左边,
∴A(-1,0),(3,0).
令x=0,则y=-1,故该抛物线与y轴的交点坐标是(0,-1).
又∵
>0,
∴该抛物线的开口方向向上.
结合(1)中抛物线的顶点坐标M(1,-
)作出如下图象:
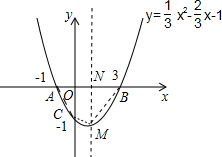 ;
;
(3)根据图示知,当x=-1或x=3时,y=0;
当x<-1或x>3时,y>0;
当-1<x<3时,y<0;
(4)如上图,连接AC、CM、MB.
则有S四边形ABMC=S△AOC+S△BMN+S梯形MNOC
=
OA•OC+
BN•MN+
(OC+MN)•ON
=
×1×1+
×1×
+
×(1+
)×1
=
.
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
∴它的顶点M的坐标为:(1,-
| 4 |
| 3 |
(2)令y=0,则
| 1 |
| 3 |
| 2 |
| 3 |
整理,得
(x-3)(x+1)=0,
解得 x1=3,x2=-1,
∵该抛物线与x轴的两个交点A在B的左边,
∴A(-1,0),(3,0).
令x=0,则y=-1,故该抛物线与y轴的交点坐标是(0,-1).
又∵
| 1 |
| 3 |
∴该抛物线的开口方向向上.
结合(1)中抛物线的顶点坐标M(1,-
| 4 |
| 3 |
 ;
;(3)根据图示知,当x=-1或x=3时,y=0;
当x<-1或x>3时,y>0;
当-1<x<3时,y<0;
(4)如上图,连接AC、CM、MB.
则有S四边形ABMC=S△AOC+S△BMN+S梯形MNOC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
=
| 7 |
| 3 |
点评:此题考查了二次函数的性质与图象,考查了通过配方法求顶点式,求顶点坐标,对称轴;还考查了根据对称轴了解二次函数的增减性及观察图象回答问题的能力.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
根据概率的含义,指出下列说法不正确的是( )
| A、不同的人做同一实验,得出某事件发生的概率不相同,因此该事件的概率不是确定的值 | ||
| B、实验的次数越多,某事件发生的概率就和该事件的概率越接近 | ||
C、某事件的概率为
| ||
| D、生活中常用“万一”这个词,从概率的含义说该事件的概率为“万分之一” |
 如图,已知二次函数y=ax2-4x+c的图象经过点A和点B.
如图,已知二次函数y=ax2-4x+c的图象经过点A和点B.