题目内容
5．一元二次方程x2-7x-2=0的实数根的情况是（ ）| A． | 有两个不相等的实数根 | B． | 有两个相等的实数根 | ||
| C． | 没有实数根 | D． | 不能确定 |
分析 先计算判别式的值，然后根据判别式的意义判断方程根的情况．
解答 解：∵△=（-7）2-4×（-2）=57＞0，
∴方程有两个不相等的实数根．
故选A．
点评 本题考查了根的判别式：一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：当△＞0时，方程有两个不相等的实数根；当△=0时，方程有两个相等的实数根；当△＜0时，方程无实数根．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
17．下列运算正确的是（ ）
| A． | （-a5）2=a10 | B． | 2a•3a2=6a2 | C． | -2a+a=-3a | D． | -6a6÷2a2=-3a3 |
2．
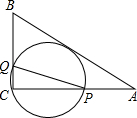如图，在△ABC中，AB=5，AC=4，BC=3，经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q，则线段PQ长度的最小值是（ ）
如图，在△ABC中，AB=5，AC=4，BC=3，经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q，则线段PQ长度的最小值是（ ）| A． | 4.75 | B． | 4.8 | C． | 5 | D． | 4$\sqrt{2}$ |