题目内容
5.已知2,4,2x,4y四个数的平均数是5,而5,7,4x,6y四个数的平均数是9,则x2+y2=13.分析 根据平均数定义得出关于x、y的方程组,求出方程组的解,最后代入求出即可.
解答 解:∵2,4,2x,4y四个数的平均数是5,而5,7,4x,6y四个数的平均数是9,
∴$\left\{\begin{array}{l}{2+4+2x+4y=4×5}\\{5+7+4x+6y=4×9}\end{array}\right.$,
解得:x=3,y=2,
∴x2+y2=32+22=13,
故答案为:13.
点评 本题考查了算术平均数的应用,能根据定义得出关于x、y的方程组是解此题的关键,难度适中.

练习册系列答案
相关题目
16.已知关于x的不等式组$\left\{\begin{array}{l}{x-a≥0}\\{4-x>1}\end{array}\right.$的整数解共有5个,则a的取值范围是( )
| A. | -3<a<-2 | B. | -3<a≤-2 | C. | -3≤a≤-2 | D. | -3≤a<-2 |
17.若不等式x-1<a的正整数解是1,2,3,则a的取值范围是( )
| A. | 2<a<3 | B. | 3<a≤4 | C. | 2<a≤3 | D. | 2≤a≤3 |
14.下列各组x、y的值,是二元一次方程x-y=5的一个解的是( )
| A. | $\left\{\begin{array}{l}x=-1\\ y=-4\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=1\\ y=4\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=1\\ y=-4\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-1\\ y=4\end{array}\right.$ |
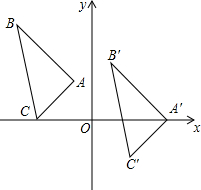 如图,△A′B′C′是由△ABC平移后得到的,已知△ABC中一点P(x0,y0)经平移后对应点为P′(x0+5,y0-2).
如图,△A′B′C′是由△ABC平移后得到的,已知△ABC中一点P(x0,y0)经平移后对应点为P′(x0+5,y0-2). 矩形ABCD中,对角线AC和BD相交于O,∠AOB=60°,AC=10.
矩形ABCD中,对角线AC和BD相交于O,∠AOB=60°,AC=10.