题目内容
如图所示①,已知AB是⊙O中一条固定的弦,点C是优弧 的一个动点(点C不与A、B重合).
的一个动点(点C不与A、B重合).
(1)设∠ACB的角平分线与劣弧![]() 交于点P,试猜想点P在
交于点P,试猜想点P在![]() 上的位置是否会随点C的运动而变化?请说明理由.
上的位置是否会随点C的运动而变化?请说明理由.

(2)如图②,设AB=8,⊙O半径为5,在(1)的条件下,四边形ACBP的面积是否是定值?若是定值,求出这个定值;若不是定值,求出四边形ACBP面积的取值范围.
答案:略
解析:
提示:
解析:
|
(1) 点P位置不会随点C的运动而变化.
∵CP平分∠ACB,∴∠ACP=∠BCP, ∴ 即P是劣弧AB的中点. ∴点P位置不会变化. (2) ∵△ABC的面积不是定值,△ABP的面积为定值∴四边形 ACBP的面积不是定值.如图②,连接 OP,交AB于E,
∵ ∴OP⊥AB, ∵OA=5. ∴ ∴ ∴当CP经过圆心O时,如图,C到AB距离最大,即△ABC的AB边上的最大高线是CE=8.
∵ AB=8,∴△ABC的最大面积是32.∴四边形 ACBP的最大面积是40.综上,四边形 ACBP的面积不是定值,它的取值范围是 |
提示:
|
(1) 点P是否会随C运动而变化位置关键是看P有何特殊性质,由PC是∠ACB的平分线可知两圆周角∠ACP和∠BCP相等,则可得 与 与 相等. 相等.
(2) 中四边形ACBP的面积可看成两个三角形面积之和,其中△ABP面积是定值,而△ACB的底是AB,高是C到AB的距离,当CP经过圆心时,C到AB的距离最大,△ABC面积最大,则四边形ACBP面积也最大. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 .
. ,PE=2.
,PE=2. .
.
 11、在直角梯形ABCD中(如图所示),已知AB∥DC,∠DAB=90°,∠ABC=60°,EF为中位线,且BC=EF=4,那么AB=( )
11、在直角梯形ABCD中(如图所示),已知AB∥DC,∠DAB=90°,∠ABC=60°,EF为中位线,且BC=EF=4,那么AB=( )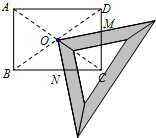 某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转(如图所示).已知AB=8,BC=10,图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.问:是否存在某一旋转位置,使得CM+CN等于
某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转(如图所示).已知AB=8,BC=10,图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.问:是否存在某一旋转位置,使得CM+CN等于 某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转(如图所示).已知AB=8,BC=10,图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.问:是否存在某一旋转位置,使得CM+CN等于
某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转(如图所示).已知AB=8,BC=10,图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.问:是否存在某一旋转位置,使得CM+CN等于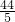 ?若存在,请求出此时DM的长;若不存在,请说明理由.
?若存在,请求出此时DM的长;若不存在,请说明理由. ?若存在,请求出此时DM的长;若不存在,请说明理由.
?若存在,请求出此时DM的长;若不存在,请说明理由.
