题目内容
11、在直角梯形ABCD中（如图所示），已知AB∥DC，∠DAB=90°，∠ABC=60°，EF为中位线，且BC=EF=4，那么AB=（ ）分析：根据已知可求得两底之和的长及腰长等于上底，从而可得到下底的长等于上底长的2倍，从而不难求得梯形的下底长．
解答：
解：作CG⊥AB于G点，
∵∠ABC=60°BC=EF=4，
∴BG=2，
设AB=x，则CD=x-2，
∵EF为中位线，
∴AB+CD=2EF，即x+x-2=8，解得x=5，
故选B．
解：作CG⊥AB于G点，∵∠ABC=60°BC=EF=4，
∴BG=2，
设AB=x，则CD=x-2，
∵EF为中位线，
∴AB+CD=2EF，即x+x-2=8，解得x=5，
故选B．
点评：此题综合运用了梯形的中位线定理、直角三角形的性质．在该图中，最关键的地方是正确的构造直角三角形．
练习册系列答案
中考解读考点精练系列答案
相关题目
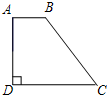如图，在直角梯形ABCD中，AB∥DC，∠D=90°，若AD=8，BC=10，则cosC的值为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
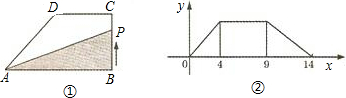
如图，在直角梯形ABCD中，AD∥BC，AB⊥BC，且AB=BC=4AD，E是AB上的一点，DE⊥EC．求证：CE平分∠BCD．
如图，在直角梯形ABCD中，∠A=∠B=90°，∠C=45°，AB=4，AD=5，把梯形沿过点D的直线折叠，使点A刚好落在BC边上，则此时折痕的长为
如图，在直角梯形ABCD中，若AD=5，点A的坐标为（-2，7），则点D的坐标为（ ）