题目内容
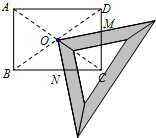某研究性学习小组在探究矩形的折纸问题时，将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转（如图所示）．已知AB=8，BC=10，图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点．问：是否存在某一旋转位置，使得CM+CN等于| 44 | 5 |
分析：延长NO交AD于点P，连接MN、MP．根据旋转的性质可得OM是PN的中垂线，在Rt△MDP和在Rt△MCN中，利用勾股定理，即可得到BN2+DM2=CN2+CM2，DM=x，CN=y，即可得到x，y的关系式，从而求解．
解答：
解：延长NO交AD于点P，连接MN、MP．
由“O为矩形ABCD的对角线交点”，通过全等或旋转对称可得BN=DP，OP=ON．（1分）
∴OM垂直平分PN．∴MP=MN．（2分）
在Rt△MDP中，MP2=DP2+DM2，
在Rt△MCN中，MN2=CN2+CM2，（3分）
又∵MP=MN，BN=DP，
∴BN2+DM2=CN2+CM2．（4分）
若设DM=x，CN=y，则CM=8-x，BN=10-y．
∴（10-y）2+x2=y2+（8-x）2．化简得y=
x+
．（6分）
∴CM+CN=8-x+y=8-x+
x+
=
-
x．（7分）
由题意得
-
x=
，（8分）
解得x=5．
∴当DM=5时，CM+CN等于
．（9分）
解：延长NO交AD于点P，连接MN、MP．由“O为矩形ABCD的对角线交点”，通过全等或旋转对称可得BN=DP，OP=ON．（1分）
∴OM垂直平分PN．∴MP=MN．（2分）
在Rt△MDP中，MP2=DP2+DM2，
在Rt△MCN中，MN2=CN2+CM2，（3分）
又∵MP=MN，BN=DP，
∴BN2+DM2=CN2+CM2．（4分）
若设DM=x，CN=y，则CM=8-x，BN=10-y．
∴（10-y）2+x2=y2+（8-x）2．化简得y=
| 4 |
| 5 |
| 9 |
| 5 |
∴CM+CN=8-x+y=8-x+
| 4 |
| 5 |
| 9 |
| 5 |
| 49 |
| 5 |
| 1 |
| 5 |
由题意得
| 49 |
| 5 |
| 1 |
| 5 |
| 44 |
| 5 |
解得x=5．
∴当DM=5时，CM+CN等于
| 44 |
| 5 |
点评：本题主要考查了旋转的性质，以及图形的旋转的性质，根据勾股定理证得BN2+DM2=CN2+CM2是解题的关键．
练习册系列答案
相关题目
