题目内容
完全相同的4个小球，上面分别标有数字1、-1、2、-2，将其放入一个不透明的盒子中摇匀，再从中随机摸球两次（第一次摸出后不放回）．把第一次、第二次摸到的球上标有的数字分别记作m、n，以m、n分别作为一个点的横坐标与纵坐标，求点（m，n）在第二象限的概率．（用树状图或列表法求解）
考点：列表法与树状图法
专题：
分析：首先根据题意画出树状图，然后由树状图求得所有等可能的结果与点（m，n）在第二象限的情况，再利用概率公式即可求得答案．
解答：解：画树状图得：
∵共有12种等可能的结果，点（m，n）在第二象限的有4种情况，
∴P（点（m，n）在第二象限）=
=
．
∵共有12种等可能的结果，点（m，n）在第二象限的有4种情况，
∴P（点（m，n）在第二象限）=
| 4 |
| 12 |
| 1 |
| 3 |
点评：本题考查的是用列表法或画树状图法求概率．注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，注意用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
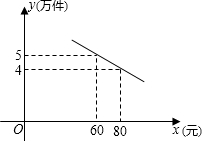某商场销售一种市场需求较大的健身器材，已知每件产品的进价为40元，每年销售该种产品的总费用（不含进货费用）总计120万元．在销售过程中发现，年销售量y（万件）与销售单价x（元/件）之间存在着如图所示的一次函数关系．若商场希望该种产品一年的销售利润为40万元，请你为商场定一个销售单价．（年销售利润=年销售额-年销售产品进货总费用-年销售总费用）
如图，AB、AC是⊙O的两条相等的弦，延长CA到点D，使AD=AC，连接DB并延长交⊙O于点E，连接CE，CE是⊙O的直径吗？为什么？