题目内容
17.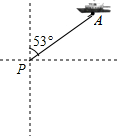 如图,一艘海轮位于灯塔P的北偏东53°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.
如图,一艘海轮位于灯塔P的北偏东53°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.(1)在图中画出点B,并求出B处与灯塔P的距离(结果取整数);
(2)用方向和距离描述灯塔P相对于B处的位置.
(参考数据:sin53°=0.80,cos53°=0.60,tan53°=0.33,$\sqrt{2}$=1.41)
分析 (1)根据方向角的定义结合已知条件在图中画出点B,作PC⊥AB于C,先解Rt△PAC,得出PC=PA•sin∠PAC=80,再解Rt△PBC,得出PB=$\sqrt{2}$PC=1.41×80≈113;
(2)由∠CBP=45°,PB≈113海里,即可得到灯塔P位于B处北偏西45°方向,且距离B处约113海里.
解答 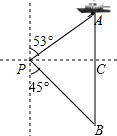 解:(1)如图,作PC⊥AB于C,
解:(1)如图,作PC⊥AB于C,
在Rt△PAC中,∵PA=100,∠PAC=53°,
∴PC=PA•sin∠PAC=100×0.80=80,
在Rt△PBC中,∵PC=80,∠PBC=∠BPC=45°,
∴PB=$\sqrt{2}$PC=1.41×80≈113,
即B处与灯塔P的距离约为113海里;
(2)∵∠CBP=45°,PB≈113海里,
∴灯塔P位于B处北偏西45°方向,且距离B处约113海里.
点评 本题考查了解直角三角形的应用-方向角问题,直角三角形,锐角三角函数的有关知识.解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.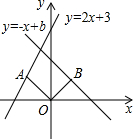 如图,在平面直角坐标系中,点A(-1,m)在直线y=2x+3上,连结OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=-x+b上,则b的值为( )
如图,在平面直角坐标系中,点A(-1,m)在直线y=2x+3上,连结OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=-x+b上,则b的值为( )
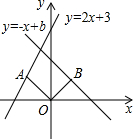 如图,在平面直角坐标系中,点A(-1,m)在直线y=2x+3上,连结OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=-x+b上,则b的值为( )
如图,在平面直角坐标系中,点A(-1,m)在直线y=2x+3上,连结OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=-x+b上,则b的值为( )| A. | -2 | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
 根据图中的信息,求梅花鹿和长颈鹿现在的高度.
根据图中的信息,求梅花鹿和长颈鹿现在的高度.


