题目内容
【题目】综合与探究
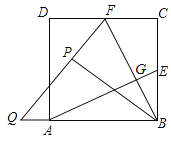
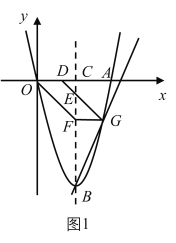
如图,已知抛物线![]() 经过点
经过点![]() ,定点为
,定点为![]() ,对称轴
,对称轴![]() 交
交![]() 轴于点
轴于点![]() .点
.点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是在
是在![]() 轴下方的抛物线对称轴上的一个动点,
轴下方的抛物线对称轴上的一个动点,![]() 交
交![]() 于点
于点![]() ,
,![]() 轴交射线
轴交射线![]() 于点
于点![]() ,作直线
,作直线![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)如图1,当点![]() 恰好落在该抛物线上时,求点
恰好落在该抛物线上时,求点![]() 的坐标;
的坐标;
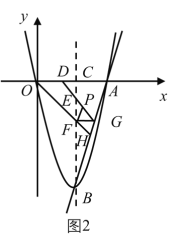
(3)如图2,当![]() 时,判断点
时,判断点![]() 是否在直线
是否在直线![]() 上,说明理由;
上,说明理由;
(4)在(3)的条件下,延长![]() 交
交![]() 于点
于点![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() ,探究四边形
,探究四边形![]() 是否为平行四边形,并说明理由.
是否为平行四边形,并说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,点
时,点![]() 在直线
在直线![]() 上.理由见解析;(4)四边形
上.理由见解析;(4)四边形![]() 是平行四边形,理由见解析
是平行四边形,理由见解析
【解析】
(1)先将点A坐标代入抛物线解析式,求出抛物线的解析式,从而求出点B的坐标;(2)先根据平行四边形的性质及抛物线的解析式求出G点的坐标,然后因为![]() ,根据平行线分线段成比例,求出CE的值,则可得E的坐标;(3)首先求出直线BG的解析式,然后检查A点是否在直线BG上;(4)根据平行四边形的判定判断四边形PFHG是否式平行四边形.
,根据平行线分线段成比例,求出CE的值,则可得E的坐标;(3)首先求出直线BG的解析式,然后检查A点是否在直线BG上;(4)根据平行四边形的判定判断四边形PFHG是否式平行四边形.
解:(1)![]() 经过点
经过点![]() ,
,
![]() ,解得
,解得![]() .
.
![]() 抛物线的表达式为
抛物线的表达式为![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
(2)![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 为平行四边形.
为平行四边形.
![]() ,
,![]()
又![]() ,
,![]() ,
,![]() .
.
![]() 点
点![]() 的横坐标为
的横坐标为![]() ,
,
![]() 点
点![]() 落在抛物线
落在抛物线![]() 上,
上,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() .
.
![]() ,
,
![]() 即
即![]() ,
,![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
(3)当![]() 时,点
时,点![]() 在直线
在直线![]() 上.
上.
理由如下:
当![]() 时,由(2)可知
时,由(2)可知![]() ,
,
![]()
设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
把![]() ,
,![]() 两点坐标代人,
两点坐标代人,
可得![]() .
.
解方程组,得![]() .
.
![]() 直线
直线![]() 的函数表达式为
的函数表达式为![]() .
.
![]() 当
当![]() 时,
时,![]() ,
,
![]() 点
点![]() 在直线
在直线![]() 上.
上.
(4)四边形![]() 是平行四边形.
是平行四边形.
理由如下:
由(3)可知点![]() 的坐标为
的坐标为![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
![]() .解得
.解得![]() .
.
![]() 直线
直线![]() 的函数表达式为
的函数表达式为![]() .
.
解方程组![]() ,解得
,解得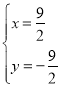
![]() 点
点![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]() 为
为![]() 的中点,
的中点,
![]()
![]() (或
(或![]() ),
),![]() .
.
![]() 四边形
四边形![]() 为平行四边形.
为平行四边形.

【题目】某服装店计划购进一批甲、乙两种款式的运动服进行销售,进价和售价如下表所示:
运动服款式 | 甲 | 乙 |
进价(元/套) | 80 | 100 |
售价(元/套) | 120 | 160 |
若购进两种款式的运动服共300套,且投入资金不超过26800元.
(1) 该服装店应购进甲款运动服至少多少套?
(2)若服装店购进甲款运动服的进价每套降低a元,并保持这两款运动服的售价不变,且最多购进240套甲款运动服.如果这批运动服售出后,服装店刚好获利18480元,求a的取值范围.