题目内容
1.已知二元一次方程组$\left\{\begin{array}{l}{x+y=5a+3}\\{x-y=3a-5}\end{array}\right.$,其中x<0,y>0,求a的取值范围,并把解集在数轴上表示出来.分析 首先解方程组求得方程组的解,然后根据x<0,y>0即可得到a的取值范围,从而求解.
解答 解:解方程组得:$\left\{\begin{array}{l}{x=4a-1}\\{y=a+4}\end{array}\right.$,
由题意得:$\left\{\begin{array}{l}{4a-1<0}\\{a+4>0}\end{array}\right.$,
解得:-4<a<$\frac{1}{4}$.
∴一元一次不等式组的解集在数轴上表示为: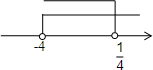 .
.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.要注意x是否取得到,若取得到则x在该点是实心的.反之x在该点是空心的.

练习册系列答案
相关题目
12.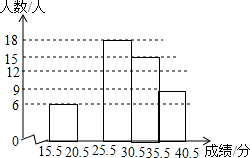 某学校为了了解八年级400名学生期末考试的体育测试成绩,从中随机抽取了部分学生的成绩(满分40分,而且成绩均为整数),绘制了频数分布表与频数分布直方图(如图).
某学校为了了解八年级400名学生期末考试的体育测试成绩,从中随机抽取了部分学生的成绩(满分40分,而且成绩均为整数),绘制了频数分布表与频数分布直方图(如图).
请结合图表信息解答下列问题:
(1)a=12,b=0.25;
(2)补全频数分布直方图;
(3)该问题中的样本容量是多少?答:60;
(4)如果成绩在30分以上(不含30分)的同学属于优良,请你估计该校八年级约有多少人达到优良水平?
 某学校为了了解八年级400名学生期末考试的体育测试成绩,从中随机抽取了部分学生的成绩(满分40分,而且成绩均为整数),绘制了频数分布表与频数分布直方图(如图).
某学校为了了解八年级400名学生期末考试的体育测试成绩,从中随机抽取了部分学生的成绩(满分40分,而且成绩均为整数),绘制了频数分布表与频数分布直方图(如图).| 分组 | 频数 | 频率 |
| 15.5~20.5 | 6 | 0.10 |
| 20.5~25.5 | a | 0.20 |
| 25.5~30.5 | 18 | 0.30 |
| 30.5~35.5 | 15 | b |
| 35.5~40.5 | 9 | 0.15 |
(1)a=12,b=0.25;
(2)补全频数分布直方图;
(3)该问题中的样本容量是多少?答:60;
(4)如果成绩在30分以上(不含30分)的同学属于优良,请你估计该校八年级约有多少人达到优良水平?
9.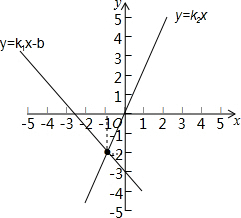 直线l1:y=k1x+b与直线l2:y-=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式组0>k2x>k1x+b的解集为( )
直线l1:y=k1x+b与直线l2:y-=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式组0>k2x>k1x+b的解集为( )
 直线l1:y=k1x+b与直线l2:y-=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式组0>k2x>k1x+b的解集为( )
直线l1:y=k1x+b与直线l2:y-=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式组0>k2x>k1x+b的解集为( )| A. | x>-1 | B. | -1<x<0 | C. | -2<x<-1 | D. | -2<x<0 |
16.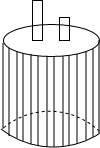 如图,两根铁棒直立于桶底水平的木桶,在桶中加入水后,一根露出水面的长度是它的$\frac{1}{3}$,另一根露出水面的长度是它的$\frac{1}{5}$.两根铁棒长度之和为220cm,求此时木桶中水的深度.如果设一根铁棒长xcm,另一根铁棒长ycm,则可列方程组为( )
如图,两根铁棒直立于桶底水平的木桶,在桶中加入水后,一根露出水面的长度是它的$\frac{1}{3}$,另一根露出水面的长度是它的$\frac{1}{5}$.两根铁棒长度之和为220cm,求此时木桶中水的深度.如果设一根铁棒长xcm,另一根铁棒长ycm,则可列方程组为( )
 如图,两根铁棒直立于桶底水平的木桶,在桶中加入水后,一根露出水面的长度是它的$\frac{1}{3}$,另一根露出水面的长度是它的$\frac{1}{5}$.两根铁棒长度之和为220cm,求此时木桶中水的深度.如果设一根铁棒长xcm,另一根铁棒长ycm,则可列方程组为( )
如图,两根铁棒直立于桶底水平的木桶,在桶中加入水后,一根露出水面的长度是它的$\frac{1}{3}$,另一根露出水面的长度是它的$\frac{1}{5}$.两根铁棒长度之和为220cm,求此时木桶中水的深度.如果设一根铁棒长xcm,另一根铁棒长ycm,则可列方程组为( )| A. | $\left\{\begin{array}{l}{x+y=220}\\{\frac{1}{3}x=\frac{1}{5}y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=220}\\{(1-\frac{1}{3})x=(1-\frac{1}{5})y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=220}\\{220-\frac{1}{3}x=220-\frac{1}{5}y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=220}\\{3x=5y}\end{array}\right.$ |
6.$\sqrt{6}$+2和$\sqrt{6}$-2的关系是( )
| A. | 互为相反数 | B. | 互为倒数 | C. | 相等 | D. | 以上都不对 |
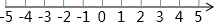 解不等式组:$\left\{\begin{array}{l}{2(x-1)≥x-4}\\{\frac{x+7}{2}>x+2}\end{array}\right.$,并把不等式组的解集表示在数轴上.
解不等式组:$\left\{\begin{array}{l}{2(x-1)≥x-4}\\{\frac{x+7}{2}>x+2}\end{array}\right.$,并把不等式组的解集表示在数轴上.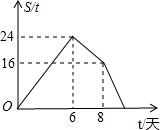 某农资销售部连续8天调进一批化肥进行销售,在开始调进化肥的第7天开始销售.若进货期间每天调入化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个销售部的化肥存量S(单位:吨)与时间t(单位:天)之间的函数关系如图所示,则该销售部这次化肥销售活动(从开始进货到销售完毕)所用时间是10天.
某农资销售部连续8天调进一批化肥进行销售,在开始调进化肥的第7天开始销售.若进货期间每天调入化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个销售部的化肥存量S(单位:吨)与时间t(单位:天)之间的函数关系如图所示,则该销售部这次化肥销售活动(从开始进货到销售完毕)所用时间是10天.
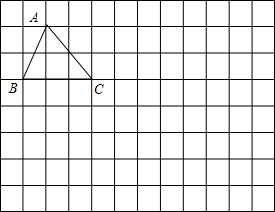 将如图所示的三角形ABC,先水平向右平移5格得三角形DEF,再竖直向下平移4格得到三角形GHQ,作出这两个三角形,并标上字母.
将如图所示的三角形ABC,先水平向右平移5格得三角形DEF,再竖直向下平移4格得到三角形GHQ,作出这两个三角形,并标上字母.