题目内容
如图，AD、BC垂直相交于点O，AB∥CD，又BC=8，AD=6，求：AB+CD的长．考点：勾股定理,平行四边形的判定与性质
专题：
分析：过点C作AD的平行线，交BA的延长线于点E，先证明四边形ADCE是平行四边形，得出CD=AE，CE=AD=6，再证明CE⊥BC，于是根据勾股定理得到BE2=BC2+CE2=100，则BE=10，进而求出AB+CD=BE=10．
解答：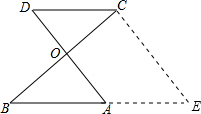
解：如图，过点C作AD的平行线，交BA的延长线于点E．
∵AB∥CD，CE∥AD，
∴四边形ADCE是平行四边形，
∴CD=AE，CE=AD=6．
∵AD⊥BC，CE∥AD，
∴CE⊥BC，
∴BE2=BC2+CE2=82+62=100，
∴BE=10，
∴AB+CD=AB+AE=BE=10．
解：如图，过点C作AD的平行线，交BA的延长线于点E．∵AB∥CD，CE∥AD，
∴四边形ADCE是平行四边形，
∴CD=AE，CE=AD=6．
∵AD⊥BC，CE∥AD，
∴CE⊥BC，
∴BE2=BC2+CE2=82+62=100，
∴BE=10，
∴AB+CD=AB+AE=BE=10．
点评：本题考查了勾股定理，平行四边形的判定与性质，平行线的性质，难度适中．准确作出辅助线是解题的关键．
练习册系列答案
相关题目
如图，P为平行四边形ABCD内一点，过点P分别作AB、AD的平行线交平行四边形于E、F、G、H四点，若SAHPE=3，SPFCG=5，则S△PBD为（ ）下列条件中，不能判断四边形ABCD是平行四边形的是（ ）
| A、AB=CD，AD∥BC |
| B、AB∥CD，AB=CD |
| C、AB=CD，AD=BC |
| D、AB∥CD，AD∥BC |
如图，在△ABC中，∠ACB=90°，AC=BC，点D在边AB上，连接CD，将线段CD绕点C顺时针旋转90°至CE位置，连接AE．求证：AB⊥AE．
如图：两张宽度都为9cm的纸条交叉重叠在一起，其中∠α=60°，求重叠（阴影）部分的面积？（结果保留根号）