题目内容
1.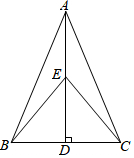 如图,在等腰△ABC中,AD是BC边上的高,点E是AD上的一点.
如图,在等腰△ABC中,AD是BC边上的高,点E是AD上的一点.(1)求证:△BEC是等腰三角形.
(2)若AB=AC=13,BC=10,点E是AD的中点,求BE的长.
分析 (1)根据等腰三角形的三线合一解答;
(2)根据等腰三角形的性质求出BD,根据勾股定理求出AD,根据勾股定理计算即可.
解答 解:(1)∵等腰△ABC,AD是BC边上的高,
∴AD为BC边上的垂直平分线,
∵E在AD上,
∴BE=CE,
∴△BEC为等腰三角形;
(2)∵AB=AC,AD为BC边上的高.
∴D为BC中点,
∴BD=$\frac{1}{2}$BC=5,
∵在Rt△ABD中,∠ADB=90°,
∴AD2+BD2=AB2,即AD2=132-52=122,
∴AD=12,
∵E为AD中点
∴DE=$\frac{1}{2}$AD=6,
∵在Rt△BDE中,∠BDE=90°.
∴BE2=DE2+BD2=52+62=($\sqrt{61}$)2
∴BE=$\sqrt{61}$.
点评 本题考查的是等腰三角形的性质、勾股定理的应用,掌握等腰三角形的三线合一是解题的关键.

练习册系列答案
相关题目
11.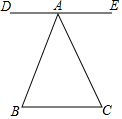 如图,ED∥BC,∠B=∠C,则下列正确的是( )
如图,ED∥BC,∠B=∠C,则下列正确的是( )
 如图,ED∥BC,∠B=∠C,则下列正确的是( )
如图,ED∥BC,∠B=∠C,则下列正确的是( )| A. | ∠BAE=∠DAC | B. | ∠BAE=∠ACB | C. | ∠ABC=∠DAC | D. | ∠BAC=∠DAC |
12.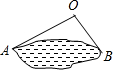 如图,为估计池塘岸边A,B的距离,小明在池塘的一侧选取一点O,测得OA=15米,OB=10米,A,B间的距离可能是( )
如图,为估计池塘岸边A,B的距离,小明在池塘的一侧选取一点O,测得OA=15米,OB=10米,A,B间的距离可能是( )
 如图,为估计池塘岸边A,B的距离,小明在池塘的一侧选取一点O,测得OA=15米,OB=10米,A,B间的距离可能是( )
如图,为估计池塘岸边A,B的距离,小明在池塘的一侧选取一点O,测得OA=15米,OB=10米,A,B间的距离可能是( )| A. | 30米 | B. | 25米 | C. | 20米 | D. | 5米 |
12.若a<0<b,则下列结论中不一定成立的是( )
| A. | a+b<0 | B. | a-b<0 | C. | ab<0 | D. | $\frac{a}{b}$<0 |
