题目内容
3.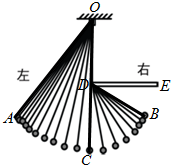 如图,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O到球心的长度为50厘米,小球在A、B两个位置时达到最高点,且最高点高度相同(不计空气阻力),在C点位置时达到最低点.达到左侧最高点时与最低点时细绳相应所成的角度为37°,细绳在右侧达到最高点时与一个水平放置的挡板DE所成的角度为30°.(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
如图,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O到球心的长度为50厘米,小球在A、B两个位置时达到最高点,且最高点高度相同(不计空气阻力),在C点位置时达到最低点.达到左侧最高点时与最低点时细绳相应所成的角度为37°,细绳在右侧达到最高点时与一个水平放置的挡板DE所成的角度为30°.(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)(1)求小球达到最高点位置与最低点位置时的高度差.
(2)求OD这段细绳的长度.
分析 (1)根据题意得出CF=OC-OF=OC-OAcos37°,进而得出答案;
(2)根据题意得出CF=CD-DF=BD-BD•cos60°=10,进而得出DB的长,进而得出答案.
解答  解:(1)连接AB交OC于点F,可知,AB⊥OC,
解:(1)连接AB交OC于点F,可知,AB⊥OC,
由题意可得:∠AOC=37°,
则CF=OC-OF=OC-OAcos37°=50-50×0.8=10(cm),
故A,C之间的高度差为10cm;
(2)由(1)知,B,C的高度差也是10cm,
故CF=CD-DF=BD-BD•cos60°=10(cm),
解得:BD=20,
则OD=OC-BD=50-20=30(cm),
答:OD这段细绳的长度为30cm.
点评 此题主要考查了解直角三角形的应用,根据题意得出OF与OA的关系是解题关键.

练习册系列答案
相关题目
14.下列计算正确的是( )
| A. | 2a-a=2 | B. | 2a+b=2ab | C. | 3x2+2x2=5x4 | D. | mn-2mn=-mn |
11.已知线段a、b、c,其中c是a、b的比例中项,若a=9cm,b=4cm,则线段c长( )
| A. | 18cm | B. | 5cm | C. | 6cm | D. | ±6cm |
 如图,线段AB=16,C是AB的中点,点D在CB上,DB=3,则线段CD的长为5.
如图,线段AB=16,C是AB的中点,点D在CB上,DB=3,则线段CD的长为5.