题目内容
8.如果A(-1,y1),B(-2,y2)是二次函数y=x2+m图象上的两个点,那么y1<y2(填“<”或者“>”)分析 根据函数解析式的特点,其对称轴为x=0,图象开口向上;利用对称轴左侧y随x的增大而减小,可判断y1<y2.
解答 解:∵二次函数y=x2+m中a=1>0,
∴抛物线开口向上.
∵x=-$\frac{b}{2a}$=0,-1<-2,
∴A(-1,y1),B(-2,y2)在对称轴的左侧,且y随x的增大而减小,
∴y1<y2.故答案为:<.
点评 本题考查的是二次函数图象上点的坐标特点,熟知二次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.下列各式中的最简分式是( )
| A. | $\frac{3y}{5}$ | B. | $\frac{{a}^{2}b+1}{a{b}^{2}-1}$ | C. | $\frac{a+b}{(a+b)^{2}}$ | D. | $\frac{{a}^{2}+2a+1}{{a}^{2}-1}$ |
20.下列各组运算中,结果为负数的是( )
| A. | -(-2)3 | B. | -|-3| | C. | (-2)×(-4) | D. | (-1)2 |
17. 如图,△ABC中,AB=AC,BE=EC,直接使用“SSS”可判定( )
如图,△ABC中,AB=AC,BE=EC,直接使用“SSS”可判定( )
 如图,△ABC中,AB=AC,BE=EC,直接使用“SSS”可判定( )
如图,△ABC中,AB=AC,BE=EC,直接使用“SSS”可判定( )| A. | △ABD≌△ACD | B. | △ABE≌△EDC | C. | △ABE≌△ACE | D. | △BED≌△CED |
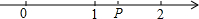 计算与化简:
计算与化简: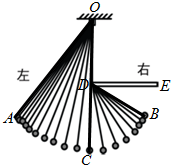 如图,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O到球心的长度为50厘米,小球在A、B两个位置时达到最高点,且最高点高度相同(不计空气阻力),在C点位置时达到最低点.达到左侧最高点时与最低点时细绳相应所成的角度为37°,细绳在右侧达到最高点时与一个水平放置的挡板DE所成的角度为30°.(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
如图,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O到球心的长度为50厘米,小球在A、B两个位置时达到最高点,且最高点高度相同(不计空气阻力),在C点位置时达到最低点.达到左侧最高点时与最低点时细绳相应所成的角度为37°,细绳在右侧达到最高点时与一个水平放置的挡板DE所成的角度为30°.(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75) 一次函数y1=kx与y2=x+a的图象如图所示,则x+a<kx<0的解集是0<x<1.
一次函数y1=kx与y2=x+a的图象如图所示,则x+a<kx<0的解集是0<x<1.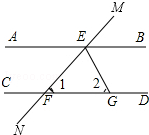 请补全说理过程:
请补全说理过程: