题目内容
 △ABC和△DCE是等边三角形,则在右图中,△ACE绕着________点________旋转________度可得到△BCD.
△ABC和△DCE是等边三角形,则在右图中,△ACE绕着________点________旋转________度可得到△BCD.
C 逆时针方向 60
分析:先根据等边三角形的性质,运用SAS证明△ACE≌△BCD,再由旋转的定义即可求解.
解答:∵△ABC和△DCE是等边三角形,
∴CA=CB,CE=CD,∠DCE=∠ACB=60°,
∴∠ACE=∠BCD=60°+∠ACD.
∵在△ACE与△BCD中,
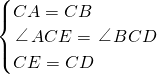 ,
,
∴△ACE≌△BCD(SAS),
∴△ACE绕点C逆时针方向旋转60度可得到△BCD.
故答案为:C;逆时针方向;60.
点评:本题考查了旋转的定义,等边三角形的性质和三角形全等的判定定理,难度适中.
分析:先根据等边三角形的性质,运用SAS证明△ACE≌△BCD,再由旋转的定义即可求解.
解答:∵△ABC和△DCE是等边三角形,
∴CA=CB,CE=CD,∠DCE=∠ACB=60°,
∴∠ACE=∠BCD=60°+∠ACD.
∵在△ACE与△BCD中,
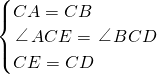 ,
,∴△ACE≌△BCD(SAS),
∴△ACE绕点C逆时针方向旋转60度可得到△BCD.
故答案为:C;逆时针方向;60.
点评:本题考查了旋转的定义,等边三角形的性质和三角形全等的判定定理,难度适中.

练习册系列答案
相关题目
 17、△ABC和△DCE是等边三角形,则在此图中,△ACE绕着
17、△ABC和△DCE是等边三角形,则在此图中,△ACE绕着 17、如图,△ABC和△DCE是等边三角形,△ACE绕着
17、如图,△ABC和△DCE是等边三角形,△ACE绕着 △ABC和△DCE是等边三角形,则在右图中,△ACE绕着
△ABC和△DCE是等边三角形,则在右图中,△ACE绕着
