题目内容
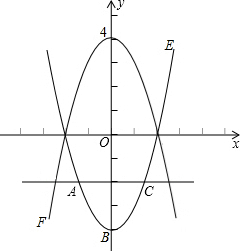 如图,已知抛物线E:y=x2-4的图象与直线l:y=-2交于A、C两点,B为抛物线y=x2-4的顶点,抛物线F与E关于x轴对称.
如图,已知抛物线E:y=x2-4的图象与直线l:y=-2交于A、C两点,B为抛物线y=x2-4的顶点,抛物线F与E关于x轴对称.(1)求抛物线F的关系式;
(2)x轴下方的F上是否存在一点D,使以A,B,C,D为顶点的四边形是平行四边形?若存在,求点D的坐标;若不存在,请说明理由;
(3)将抛物线E的关系式改为y=ax2+c(a>0,c≠0),直线l的关系式改为y=-
| c |
| 2 |
考点:二次函数综合题
专题:
分析:(1)利用关于x轴对称的两点横坐标不变,纵坐标互为相反数解答即可;
(2)先由抛物线E的解析式为y=x2-4,求出A,C,B三点的坐标,得到AC=2
,再根据平行四边形的性质,得出当D点在x轴下方时,D点坐标为(-2
,-4)或(2
,-4),再把这两个点代入抛物线F的解析式中,发现这两个点满足F的解析式,从而得出所求点D的坐标;
(3)把E的解析式系数用a代替,借助参数a来求证这两个点.方法跟前面一样.
(2)先由抛物线E的解析式为y=x2-4,求出A,C,B三点的坐标,得到AC=2
| 2 |
| 2 |
| 2 |
(3)把E的解析式系数用a代替,借助参数a来求证这两个点.方法跟前面一样.
解答:解:(1)∵抛物线F与E关于x轴对称,抛物线E的解析式为y=x2-4,
∴抛物线F的解析式为-y=x2-4,即y=-x2+4;
(2)存在点D,而且还是两个.
将y=-2代入y=x2-4,得x2-4=-2,
解得x=±
,
所以A点坐标为(-
,-2),C点坐标为(
,-2),
抛物线y=x2-4的顶点B的坐标为(0,-4),
所以AC=2
,
所以在x轴下方,当D点坐标为(-2
,-4)或(2
,-4)时,以A,B,C,D为顶点的四边形是平行四边形.
将(-2
,-4)代入抛物线F的解析式y=-x2+4,得左边=-4,右边=-(-2
)2+4=-4,左边=右边,点(-2
,-4)在抛物线F上,
同理,将(2
,-4)代入抛物线F的解析式y=-x2+4,得左边=-4,右边=-(2
)2+4=-4,左边=右边,点(2
,-4)在抛物线F上.
综上所述,所求点D的坐标为(-2
,-4)或(2
,-4);
 (3)不存在点D,理由如下:
(3)不存在点D,理由如下:
如图,将y=-
代入y=ax2+c,得ax2+c=-
,
整理,得x2=-
,
∵a>0,c≠0,
∴c>0时原方程无解,点D不存在;
c<0时,解得x=±
,此时A点坐标为(-
,-
),C点坐标为(
,-
),A,C两点均在x轴上方.
抛物线E:y=ax2+c的顶点B的坐标为(0,c),B在x轴下方,抛物线F的解析式为y=-ax2-c.
∵AC=
,
∴在x轴下方,当D点坐标为(-
,c)或(
,c)时,以A,B,C,D为顶点的四边形是平行四边形.
将(-
,c)代入抛物线F的解析式y=-ax2-c,得左边=c,右边=-a(-
)2-c=5c,左边≠右边,点(-
,c)不在抛物线F上,
同理,将(
,c)代入抛物线F的解析式y=-ax2-c,得左边=c,右边=-a(
)2-c=5c,左边≠右边,点(
,c)不在抛物线F上.
综上所述,所求点D的坐标不存在.
∴抛物线F的解析式为-y=x2-4,即y=-x2+4;
(2)存在点D,而且还是两个.
将y=-2代入y=x2-4,得x2-4=-2,
解得x=±
| 2 |
所以A点坐标为(-
| 2 |
| 2 |
抛物线y=x2-4的顶点B的坐标为(0,-4),
所以AC=2
| 2 |
所以在x轴下方,当D点坐标为(-2
| 2 |
| 2 |
将(-2
| 2 |
| 2 |
| 2 |
同理,将(2
| 2 |
| 2 |
| 2 |
综上所述,所求点D的坐标为(-2
| 2 |
| 2 |
 (3)不存在点D,理由如下:
(3)不存在点D,理由如下:如图,将y=-
| c |
| 2 |
| c |
| 2 |
整理,得x2=-
| 3c |
| 2a |
∵a>0,c≠0,
∴c>0时原方程无解,点D不存在;
c<0时,解得x=±
| ||
| 2a |
| ||
| 2a |
| c |
| 2 |
| ||
| 2a |
| c |
| 2 |
抛物线E:y=ax2+c的顶点B的坐标为(0,c),B在x轴下方,抛物线F的解析式为y=-ax2-c.
∵AC=
| ||
| a |
∴在x轴下方,当D点坐标为(-
| ||
| a |
| ||
| a |
将(-
| ||
| a |
| ||
| a |
| ||
| a |
同理,将(
| ||
| a |
| ||
| a |
| ||
| a |
综上所述,所求点D的坐标不存在.
点评:本题是二次函数的综合题型,其中涉及到的知识点有二次函数图象与几何变换,二次函数图象上点的坐标特征,平行四边形的性质,综合性较强,难度适中.运用数形结合是解题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
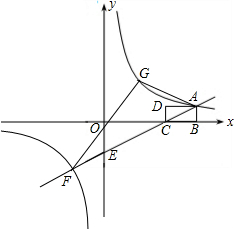 如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象经过点A、C,并与y轴交于点E.反比例函数y=
如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象经过点A、C,并与y轴交于点E.反比例函数y=
 画出如图立体图形从正面、左面和上面看到的形状图.
画出如图立体图形从正面、左面和上面看到的形状图.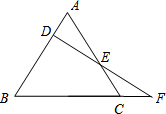 如图,F是等腰三角形ABC的底边BC的延长上一点,且FD⊥AB,垂足为D,交AC于点E,若已知∠F=35°,则∠A=
如图,F是等腰三角形ABC的底边BC的延长上一点,且FD⊥AB,垂足为D,交AC于点E,若已知∠F=35°,则∠A=