题目内容
3.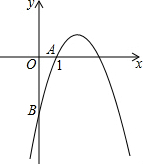 如图,抛物线y=-x2+5x+n经过点A(1,0),与y轴交于点B.
如图,抛物线y=-x2+5x+n经过点A(1,0),与y轴交于点B.(1)求抛物线的解析式;
(2)P是y轴上一点,且△PAB是以AB为腰的等腰三角形,试求P点坐标.
(3)将抛物线y=-x2+5x+n沿着坐标轴方向经过怎样的一次平移可以使它使它经过原点.
分析 (1)将A点的坐标代入抛物线中,即可得出二次函数的解析式.
(2)本题要分两种情况进行讨论:
①PA=AB,先根据抛物线的解析式求出B点的坐标,即可得出OB的长,进而可求出AB的长,也就知道了PB的长,由此可求出P点的坐标;
②PB=AB,此时P与A关于y轴对称,由此可求出P点的坐标.
(3)观察图象结合解析式写出答案即可.
解答 解:(1)∵抛物线y=-x2+5x+n经过点A(1,0)
∴n=-4
∴y=-x2+5x-4;
(2)∵抛物线的解析式为y=-x2+5x-4,
∴令x=0,则y=-4,
∴B点坐标(0,-4),AB=$\sqrt{17}$,
①当PA=AB时,PA=AB,则有OB=OP
此时P(0,4)
②当PB=AB时,|PB|=$\sqrt{17}$,
故P(0,$\sqrt{17}-4$);P(0,-$\sqrt{17}-4$)
③P为顶点时,PA=PB,点P在AB的垂直平分线与y轴交点处(0,-$\frac{15}{8}$)
因此P点的坐标为P(0,4);P(0,$\sqrt{17}-4$);P(0,-$\sqrt{17}-4$);P(0,-$\frac{15}{8}$)
(3)将抛物线y=-x2+5x-4沿着坐标轴方向向左平移1个,或向左平移4个,或向上平移4个均平移可以使它使它经过原点.
点评 本题考查了二次函数解析式的确定、等腰三角形的性质等知识点,主要考查学生分类讨论、数形结合的数学思想方法.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
14.下列运算正确的是( )
| A. | (a-b)2=a2-b2 | B. | (a+b)2=a2+ab+b2 | C. | (1+a)(a-1)=a2-1 | D. | (a+b)(b-a)=a2-b2 |
11.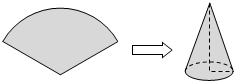 用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )
用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )
 用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )
用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )| A. | 4cm | B. | 4$\sqrt{2}$cm | C. | 3$\sqrt{2}$cm | D. | $\sqrt{2}$cm |
13.计算3x2-2xy-y2与8x2-3xy+y2的差,结果正确的是( )
| A. | -2x2-xy-3y2 | B. | 2x2+xy+3y2 | C. | -8x2+3xy-y2 | D. | -5x2+xy-2y2 |

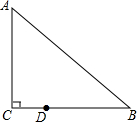 如图,在Rt△ABC中,∠C=90°,∠B=40°,点D在边BC上,BD=2CD.把△ABC绕点D逆时针旋转m度后(0<m<360),如果点B恰好落在初始Rt△ABC的边所在的直线上,那么m=100°或120°.
如图,在Rt△ABC中,∠C=90°,∠B=40°,点D在边BC上,BD=2CD.把△ABC绕点D逆时针旋转m度后(0<m<360),如果点B恰好落在初始Rt△ABC的边所在的直线上,那么m=100°或120°.