题目内容
4.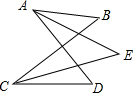 如图,AD与BC相交,连接AB、CD,AE平分∠BAD,CE平分∠BCD.若∠B=40°,∠D=50°,则∠E=45°; 若∠B=x°,∠D=y°,则∠E=$\frac{1}{2}$(x+y)°.
如图,AD与BC相交,连接AB、CD,AE平分∠BAD,CE平分∠BCD.若∠B=40°,∠D=50°,则∠E=45°; 若∠B=x°,∠D=y°,则∠E=$\frac{1}{2}$(x+y)°.
分析 根据角平分线的定义得到∠1=∠2,∠3=∠4,再根据(1)中的结论得到∠1+∠B=∠3+∠E,∠2+∠E=∠4+∠D,两等式相减得到∠B-∠E=∠E-∠D,由此可得出结论.
解答 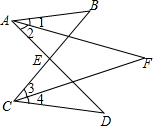 解:∵∠DAB和∠BCD的平分线AE和CE相交于点F,
解:∵∠DAB和∠BCD的平分线AE和CE相交于点F,
∴∠1=∠2,∠3=∠4,
∵∠1+∠B=∠3+∠E,∠2+∠E=∠4+∠D,
∴∠B-∠E=∠E-∠D,即∠E=$\frac{1}{2}$(∠D+∠B),
∵∠B=40°,∠D=50°,
∴∠E=45°,
∵∠B=x°,∠D=y°,
∴∠E=$\frac{1}{2}$(x+y)°,
故答案为:45°,$\frac{1}{2}$(x+y)°.
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
14.2017年1月17日我国工信部已经印发《软件和信息技术服务业发展规划(2016-2020年)》,提出到2020年,我国软件和信息技术服务业收入将突破8万亿元,8万亿元用科学记数法表示为( )
| A. | 8×1012元 | B. | 80000×108元 | C. | 8×1011元 | D. | 8×108元 |
15.下列计算正确的是( )
| A. | (a2)3=a5 | B. | a2•a3=a6 | C. | a5÷a3=a2 | D. | (a+2a)2=4a2 |
19.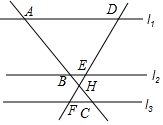 如图,直线l1∥l2∥l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,如果AB=5,BH=1,CH=2,那么$\frac{EF}{DE}$的值等于( )
如图,直线l1∥l2∥l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,如果AB=5,BH=1,CH=2,那么$\frac{EF}{DE}$的值等于( )
 如图,直线l1∥l2∥l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,如果AB=5,BH=1,CH=2,那么$\frac{EF}{DE}$的值等于( )
如图,直线l1∥l2∥l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,如果AB=5,BH=1,CH=2,那么$\frac{EF}{DE}$的值等于( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
13.从2开始,连续的偶数相加,它们和的情况如表:
(1)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=n(n+1);
(2)如下数表是由从1开始的连续自然数组成,观察规律:
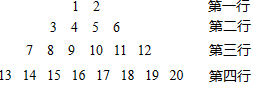
①第n行的第一个数可用含n的式子表示为:n2-n+1;
②如果某行的第一个数为157,求其所在的行数.
| 加数的个数n | S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=15=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
(2)如下数表是由从1开始的连续自然数组成,观察规律:
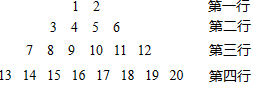
①第n行的第一个数可用含n的式子表示为:n2-n+1;
②如果某行的第一个数为157,求其所在的行数.
14. 已知:正方体展开图(如图所示)相对面上的数值相等,那么x的值等于( )
已知:正方体展开图(如图所示)相对面上的数值相等,那么x的值等于( )
 已知:正方体展开图(如图所示)相对面上的数值相等,那么x的值等于( )
已知:正方体展开图(如图所示)相对面上的数值相等,那么x的值等于( )| A. | -1 | B. | a-2 | C. | -1或2 | D. | 1或-2 |
 如图,求证:∠BDC=∠A+∠B+∠C.
如图,求证:∠BDC=∠A+∠B+∠C.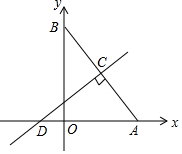 已知两直线l1:y1=k1x+b1,l2:y2=k2x+b2,若l1⊥l2,则有k1•k2=-1.
已知两直线l1:y1=k1x+b1,l2:y2=k2x+b2,若l1⊥l2,则有k1•k2=-1.