题目内容
下列计算正确的是( )
|
| A. |
| B. | 3﹣1=﹣3 | C. | (a4)2=a8 | D. | a6÷a2=a3 |
C

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
如图,观察二次函数y=ax2+bx+c的图象,下列结论:
①a+b+c>0,②2a+b>0,③b2﹣4ac>0,④ac>0.
其中正确的是( )

|
| A. | ①② | B. | ①④ | C. | ②③ | D. | ③④ |
下列说法错误的是( )
|
| A. | “伊利”纯牛奶消费者服务热线是4008169999,该十个数的中位数为7 |
|
| B. | 服装店老板最关心的是卖出服装的众数 |
|
| C. | 要了解全市初三近4万名学生2015年中考数学成绩情况,适宜采用全面调查 |
|
| D. | 条形统计图能够显示每组中的具体数据,易于比较数据之间的差别 |

 A,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左导游依次记为S1、S2、S3、…Sn,则Sn的值为 (用含n的代数式表示,n为正整数).
A,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左导游依次记为S1、S2、S3、…Sn,则Sn的值为 (用含n的代数式表示,n为正整数).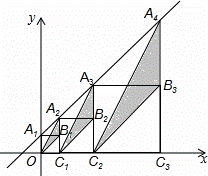

 ;
; 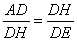 ,即
,即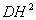 =AD×DE.
=AD×DE.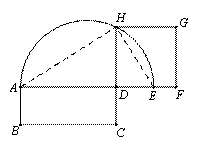
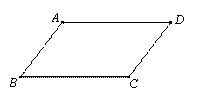
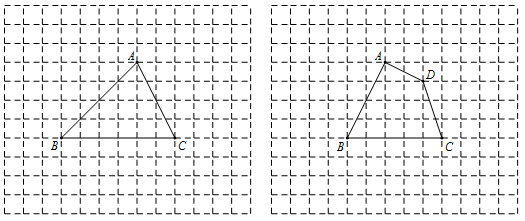
 转60°得到△AED,若线段AB=3,则BE= .
转60°得到△AED,若线段AB=3,则BE= .
 钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).
钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).