题目内容
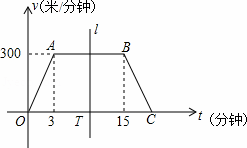
“低碳生活,绿色出行”的理念正逐渐被人们所接受,越来越多的人选择骑自行车上下班.王叔叔某天骑自行车上班从家出发到单位过程中行进速度v(米/分钟)随时间t(分 钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).
钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).
(1)①当t=2分钟时,速度v= 200 米/分钟,路程s= 200 米;
②当t=15分钟时,速度v= 300 米/分钟,路程s= 4050 米.
(2)当0≤t≤3和3<t≤15时,分别求出路程s(米)关于时间t(分钟)的函数解析式;
(3)求王叔叔该天上班从家出发行进了750米时所用的时间t.
解:(1)①直线OA的解析式为:y= t=100t,
t=100t,
把t=2代入可得:y=200;
路程S= =200,
=200,
故答案为:200;200;
②当t=15时,速度为定值=300,路程= ,
,
故答案为:300;4050;
(2)①当0≤t≤3,设直线OA的解析式为:y=kt,由图象可知点A(3,300),
∴300=3k,
解得:k=100,
则解析式为:y=100t;
设l与OA的交点为P,则P(t,100t),
∴s= ,
,
②当3<t≤15时,设l与AB的交点为Q,则Q(t,300),
∴S= ,
,
(3)∵当0≤t≤3,S最大=50×9=450,
∵750>50,
∴当3<t≤15时,450<S≤4050,
则令750=300t﹣450,
解得:t=4.
故王叔叔该天上班从家出发行进了750米时所用的时间4分钟.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案下列计算正确的是( )
|
| A. |
| B. | 3﹣1=﹣3 | C. | (a4)2=a8 | D. | a6÷a2=a3 |
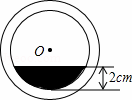
将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )
|
| A. | ( | B. | ( | C. | ( | D. | ( |
下列图形中,是中心对称图形的为( )
|
| A. |
| B. |
| C. |
| D. |
|
如图,已知扇形AOB的半径为2,圆心角为90°,连接AB,则图中阴影部分的面积是( )

|
| A. | π﹣2 | B. | π﹣4 | C. | 4π﹣2 | D. | 4π﹣4 |
一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:
| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 |
| 13元 |
(1)如果甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱,请你计算出经销商能盈利多少元?
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?

 =
= ﹣1.
﹣1. π﹣4
π﹣4 )cm2
)cm2 π﹣4
π﹣4 )cm2
)cm2 π﹣2
π﹣2




 9元
9元