题目内容
 如图,用两根长度均为lcm的绳子,分别围成一个正方形和圆.
如图,用两根长度均为lcm的绳子,分别围成一个正方形和圆.(1)如果要使正方形的面积不大于25cm2,那么绳长l应满足怎样的关系式?
(2)如果要使圆的面积不小于100cm2,那么绳长l应满足怎样的关系式?
考点:算术平方根
专题:
分析:(1)先求出边长,再求出正方形面积的范围,即可求出l满足的关系式;
(2)先求出圆的半径,再求出圆的面积范围,即可求出l满足的关系式.
(2)先求出圆的半径,再求出圆的面积范围,即可求出l满足的关系式.
解答:解:(1)∵正方形的边长为
,
∴(
)2≤25,
∴
≤5,
∴l≤20,
∴0≤l≤20;
(2)设半径为r,
∵2πr=l,
∴r=
,
∵π•(
)2=
≥100,
∴l2≥400π,l≥20
,
∴0≤l≤20
.
| l |
| 4 |
∴(
| l |
| 4 |
∴
| l |
| 4 |
∴l≤20,
∴0≤l≤20;
(2)设半径为r,
∵2πr=l,
∴r=
| l |
| 2π |
∵π•(
| l |
| 2π |
| l2 |
| 4π |
∴l2≥400π,l≥20
| π |
∴0≤l≤20
| π |
点评:本题考查了算术平方根和正方形、圆的面积的计算方法;掌握周长和边长、半径的关系是解题的关键.

练习册系列答案
相关题目
 已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2,求证:∠B=∠ADE.
已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2,求证:∠B=∠ADE. 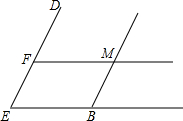 如图,已知AB∥DE,FM∥EC,∠ABC=65°,求∠EFM的度数.
如图,已知AB∥DE,FM∥EC,∠ABC=65°,求∠EFM的度数. 如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=3,CD=2.求AB的长.
如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=3,CD=2.求AB的长. 某单位冬天储备了一定数量的煤,每天所用煤的吨数y与所用的天数x满足函数关系式y=
某单位冬天储备了一定数量的煤,每天所用煤的吨数y与所用的天数x满足函数关系式y= 某县“贡江新区”位于贡江南岸(如图),由长征出发地体验区、文教体育综合区、贡江新城三大板块组成,与贡江北岸老城区相呼应,构建成“一江两岸”的城市新格局,为建设河堤漫步休闲通道,贡江新区现有一段长为180米的河堤整治任务,由A、B两个工程队先后接力完成,A工程队每天整治12米,B工程队每天整治8米,共用时20天.
某县“贡江新区”位于贡江南岸(如图),由长征出发地体验区、文教体育综合区、贡江新城三大板块组成,与贡江北岸老城区相呼应,构建成“一江两岸”的城市新格局,为建设河堤漫步休闲通道,贡江新区现有一段长为180米的河堤整治任务,由A、B两个工程队先后接力完成,A工程队每天整治12米,B工程队每天整治8米,共用时20天.