题目内容
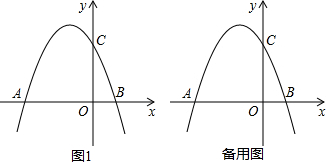
如图1,抛物线y=-x2+bx+c交x轴于点A、B,交y轴于点C,其中点B坐标为(1,0),同时抛物线还经过点(-2,3).
(1)求抛物线的解析式;
(2)是否存在直线y=kx+n(k≠0)与抛物线交于点M、N,使y轴平分△CMN的面积?若存在,求出k、n应满足的条件;若不存在,请说明理由;
(3)设抛物线的对称轴与抛物线交于点E,与x轴交于点H,连接EC、EO,将抛物线向下平移m(m>0)个单位,当EO平分∠CEH时,求m的值.
(1)求抛物线的解析式;
(2)是否存在直线y=kx+n(k≠0)与抛物线交于点M、N,使y轴平分△CMN的面积?若存在,求出k、n应满足的条件;若不存在,请说明理由;
(3)设抛物线的对称轴与抛物线交于点E,与x轴交于点H,连接EC、EO,将抛物线向下平移m(m>0)个单位,当EO平分∠CEH时,求m的值.

考点:二次函数综合题
专题:
分析:(1)把点B(1,0),点(-2,3)代入抛物线y=-x2+bx+c求出b、c的值,进而可得出结论;
(2)假设存在满足条件的直线y=kx+b(k≠0),联立直线与抛物线的解析式得出关于x的一元二次方程,根据要使y轴平分△CMN的面积,则M、N两点的横坐标互为相反数,根据根与系数的关系即可得出k、n应满足的条件;
(3)根据抛物线平移的性质可知抛物线向下平移m个单位后,E为(-1,4-m),C为(0,3-m),故可得出EC=
,再根据CO∥EH可知当CO=CE=
时,∠CEO=∠COE=∠OCH,根据两点间的距离公式即可得出m的值.
(2)假设存在满足条件的直线y=kx+b(k≠0),联立直线与抛物线的解析式得出关于x的一元二次方程,根据要使y轴平分△CMN的面积,则M、N两点的横坐标互为相反数,根据根与系数的关系即可得出k、n应满足的条件;
(3)根据抛物线平移的性质可知抛物线向下平移m个单位后,E为(-1,4-m),C为(0,3-m),故可得出EC=
| 2 |
| 2 |
解答:解:(1)将点B(1,0),点(-2,3)代入抛物线y=-x2+bx+c中,得
,解得
∴抛物线的解析式为y=-x2-2x+3;
(2)假设存在满足条件的直线y=kx+b(k≠0).
由题意得,
①-②得,x2+(k+2)x+n-3=0,③
要使y轴平分△CMN的面积,则M、N两点的横坐标互为相反数,
∴方程③满足
,
解得k=-2,n<3.即存在满足条件的直线y=kx+n(k≠0).
(3)∵抛物线向下平移m个单位后,E为(-1,4-m),C为(0,3-m),
∴EC=
.
∵CO∥EH,
∴当CO=CE=
时,∠CEO=∠COE=∠OCH,
∴3-m=
,或m-3=
,即m=3-
或m=3+
.
|
|
∴抛物线的解析式为y=-x2-2x+3;
(2)假设存在满足条件的直线y=kx+b(k≠0).
由题意得,
|
①-②得,x2+(k+2)x+n-3=0,③
要使y轴平分△CMN的面积,则M、N两点的横坐标互为相反数,
∴方程③满足
|
解得k=-2,n<3.即存在满足条件的直线y=kx+n(k≠0).
(3)∵抛物线向下平移m个单位后,E为(-1,4-m),C为(0,3-m),
∴EC=
| 2 |
∵CO∥EH,
∴当CO=CE=
| 2 |
∴3-m=
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题考查的是二次函数综合题,涉及到用待定系数法求二次函数的解析式、二次函数的图象与几何变换等知识,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平面直角坐标系中,点A,B分别在x轴、y轴的正半轴上,OA=4,AB=5.点D在反比例函数y=
如图,在平面直角坐标系中,点A,B分别在x轴、y轴的正半轴上,OA=4,AB=5.点D在反比例函数y= 为提高居民的节水意识,向阳小区开展了“建设节水型社区,保障用水安全”为主题的节水宣传活动,小莹同学积极参与小区的宣传活动,并对小区300户家庭用水情况进行了抽样调查,他在300户家庭中,随机调查了50户家庭5月份的用水量情况,结果如图所示.
为提高居民的节水意识,向阳小区开展了“建设节水型社区,保障用水安全”为主题的节水宣传活动,小莹同学积极参与小区的宣传活动,并对小区300户家庭用水情况进行了抽样调查,他在300户家庭中,随机调查了50户家庭5月份的用水量情况,结果如图所示.
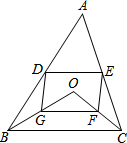 D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.