��Ŀ����
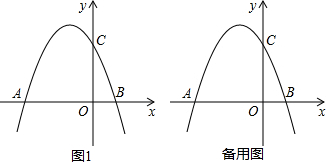
��ͼ1����֪������y=a��x-
��2+c��x�ύ��A��B���㣬��y�ύ���C��B������Ϊ��6��0����C������Ϊ��0��-3������P���߶�AB�ϵ�һ�����㣨��P����A��B�����غϣ����ڵ�P�˶������У�ʼ����һ������P�Һ�y��ƽ�е�ֱ��Ҳ��֮�˶�����ֱ���������ߵĽ���ΪM����ֱ��BC�Ľ���ΪN��
��1������������ߵĺ�������ʽ��
��ֱ��д��ֱ��BC�ĺ�������ʽ��
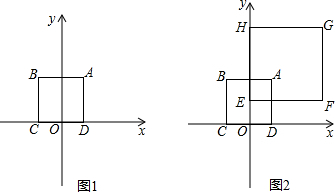
��2������ͼ2������MO��MB��ON�����ı���OMBN�����ΪS���ڵ�P���˶������У�S�Ƿ�������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
�ڵ�S��ֵ���ʱ���������ߵĶԳ������Ƿ����һ��F��ʹ��MNE���ܳ���С�������ڣ��������E�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ3������N��NH��y���ڵ�H������MH���ڵ�P���˶������У�����MNH�͡�OBC����ʱ�������M�����꣮

| 7 |
| 2 |
��1������������ߵĺ�������ʽ��
��ֱ��д��ֱ��BC�ĺ�������ʽ��
��2������ͼ2������MO��MB��ON�����ı���OMBN�����ΪS���ڵ�P���˶������У�S�Ƿ�������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
�ڵ�S��ֵ���ʱ���������ߵĶԳ������Ƿ����һ��F��ʹ��MNE���ܳ���С�������ڣ��������E�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ3������N��NH��y���ڵ�H������MH���ڵ�P���˶������У�����MNH�͡�OBC����ʱ�������M�����꣮

���㣺���κ����ۺ���
ר�⣺�ۺ���
��������1���ٽ�B�㡢C���������룬���ô���ϵ������ȷ�������ߵĺ�������ʽ������B��C��������꣬�ɵ�ֱ��BC�ĺ�������ʽ��
��2������P��x��0������M��x��-
x2+
x-3����N��x��
x-3������ʾ��MN���̶��ó�S�ı���ʽ�������䷽������ֵ���ɣ�
��������ã�M��3��3����N��3��-
������M��3��3������x=
�ĶԳƵ�M1Ϊ��4��3�������ֱ��M1N�ı���ʽ�����ݵ�F�ĺ�����Ϊ
���������F�������꣬�̶��ó���E�����꣮
��3��������������ۣ��١�NMH�ס�OBC���ڡ�NMH�ס�OCB�����ݶ�Ӧ�߳ɱ������x��ֵ���̶��ɵõ�M�����꣮
��2������P��x��0������M��x��-
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
��������ã�M��3��3����N��3��-
| 3 |
| 2 |
| 7 |
| 2 |
| 7 |
| 2 |
��3��������������ۣ��١�NMH�ס�OBC���ڡ�NMH�ס�OCB�����ݶ�Ӧ�߳ɱ������x��ֵ���̶��ɵõ�M�����꣮
����⣺��1���ٽ���B��6��0������C��0��-3�����������߽���ʽ�ɵã�
��
��ã�
��
��y=-
��x-
��+
��
����ֱ��BC�Ľ���ʽΪy=kx+b��
��
��
��ã�
��
��ֱ��BC�Ľ���ʽΪ��y=
x-3��
��2������P��x��0������M��x��-
x2+
x-3����N��x��
x-3����
��MN=-
x2+
x-3-��
x-3��=-
x2+3x��
S=
��-
x2+3x����6
=-
x2+9x
=-
��x2-6x+9-9��
=-
��x-3��2+
��
��-
��0��
�൱x=3ʱ��S���=
��
��������ã�M��3��3����N��3��-
����
M��3��3������x=
�ĶԳƵ�M1Ϊ��4��3����
��ֱ��M1N�ı���ʽΪy=mx+n������4��3������3��-
������ã�
��
��ã�
��
��y=
x-15
��x=
��
��y=
��
��F��
��
����
��3������NMH�ס�OBC����
=
=2��
��ã�x1=0����ȥ����x2=2��
��M��2��2����
����NMH�ס�OCB����
=
=
��
��ã�x1=0����ȥ����x2=5��
��M��5��2����
������������M��������5��2����2��2����
|
��ã�
|
��y=-
| 1 |
| 2 |
| 7 |
| 2 |
| 25 |
| 8 |
����ֱ��BC�Ľ���ʽΪy=kx+b��
��
|
��ã�
|
��ֱ��BC�Ľ���ʽΪ��y=
| 1 |
| 2 |
��2������P��x��0������M��x��-
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
��MN=-
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
S=
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 3 |
| 2 |
=-
| 3 |
| 2 |
=-
| 3 |
| 2 |
| 27 |
| 2 |
��-
| 3 |
| 2 |
�൱x=3ʱ��S���=
| 27 |
| 2 |
��������ã�M��3��3����N��3��-
| 3 |
| 2 |
M��3��3������x=
| 7 |
| 2 |
��ֱ��M1N�ı���ʽΪy=mx+n������4��3������3��-
| 3 |
| 2 |
|
��ã�
|
��y=
| 9 |
| 2 |
��x=
| 7 |
| 2 |
��y=
| 3 |
| 4 |
��F��
| 7 |
| 2 |
| 3 |
| 4 |
��3������NMH�ס�OBC����
-
| ||
| x |
| 6 |
| 3 |
��ã�x1=0����ȥ����x2=2��
��M��2��2����
����NMH�ס�OCB����
-
| ||
| x |
| 3 |
| 6 |
| 1 |
| 2 |
��ã�x1=0����ȥ����x2=5��
��M��5��2����
������������M��������5��2����2��2����
���������⿼���˶��κ������ۺϣ��漰�˴���ϵ������������ʽ���䷽������κ�����ֵ��������Գ������·����֪ʶ���ۺϵ�֪ʶ��϶࣬�����Ĺؼ������ν��˼�뼰��������˼������ã��ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ