题目内容
20.已知关于x的方程 kx2-2(k+1)x+k-1=0 有两个不相等的实数根,(1)求k的取值范围;
(2)是否存在实数k,使得此方程的有一个实数根等于4?若存在,求出k的值和方程的另一个根;若不存在,说明理由.
分析 (1)根据一元二次方程的定义和判别式的意义得到k≠0且△=[-2 (k+1)]2-4k( k-1)>0,然后求出两不等式的公共部分即可;
(2)根据一元二次方程的解的定义把x=1代入方程可计算出k=1,满足(1)中可的取值范围,则原方程化为x2-4x=0,然后利用因式分解法解方程即可得到方程的另一个根.
解答 解:(1)根据题意得k≠0且△=[-2 (k+1)]2-4k( k-1)>0,
解得k>$-\frac{1}{3}$且k≠0;
(2)存在.
将x=4代入原方程得k×42-2 (k+1)×4+k-1=0,解得k=1,
而k>$-\frac{1}{3}$且k≠0;
∴k的值为1,
当k=1时,原方程化为x2-4x=0,解得x1=4,x2=0,
∴方程的另一个根为0.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了一元二次方程的定义.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
9.下列计算正确的是( )
| A. | a2•a3=a6 | B. | a2-b2=(a-b)2 | C. | (3b3)2=6b6 | D. | (-a)5÷(-a)3=a2 |
 列方程解应用题:以“在非洲与非洲一起胜利”为主题口号的第十九届世界杯足球决赛于2010年6月11日-7月11日在南非举行,这场足球盛宴给世界各地的球迷们带来了无限激情,某体育用品商场推出“走近南非,共享世界杯”系列促销活动.
列方程解应用题:以“在非洲与非洲一起胜利”为主题口号的第十九届世界杯足球决赛于2010年6月11日-7月11日在南非举行,这场足球盛宴给世界各地的球迷们带来了无限激情,某体育用品商场推出“走近南非,共享世界杯”系列促销活动.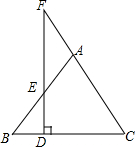 如图,已知△ABC中,AB=AC,E是AB上一点,DE⊥BC于点D,DE的延长线交CA的延长线于点F,那么△AEF是等腰三角形,为什么?
如图,已知△ABC中,AB=AC,E是AB上一点,DE⊥BC于点D,DE的延长线交CA的延长线于点F,那么△AEF是等腰三角形,为什么?