题目内容
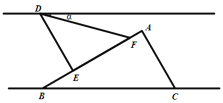
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,以每秒5个单位长度的速度沿
出发,以每秒5个单位长度的速度沿![]() 向终点
向终点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,以相同的速度沿
出发,以相同的速度沿![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() ,以
,以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() ,当点
,当点![]() 运动到终点时,整个运动停止,设矩形
运动到终点时,整个运动停止,设矩形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)①![]() 的长为 ;
的长为 ;
②用含![]() 的代数式表示线段
的代数式表示线段![]() 的长为 ;
的长为 ;
(2)当![]() 的长度为10时,求
的长度为10时,求![]() 的值;
的值;
(3)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)当过点![]() 和点
和点![]() 的直线垂直于
的直线垂直于![]() 的一边时,直接写出
的一边时,直接写出![]() 的值.
的值.
【答案】(1)①16;②3t;(2)当![]() 的长度为10时,
的长度为10时,![]() 的值为
的值为![]() ;(3)S=
;(3)S=![]() ;(4)
;(4)![]() ,
,![]()
【解析】
(1)①由勾股定理可求解;
②由锐角三角函数可求解;
(2)分两种情况讨论,由QM的长度为10,列出方程可求解;
(3)分两种情况讨论,由面积公式可求解;
(4)分两种情况讨论,由锐角三角函数可求解.
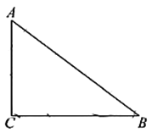
(1)①∵∠ACB=90°,AC=12,AB=20,
∴BC=![]() =
=![]() =16,
=16,
故答案为:16;
②∵sinB=![]() ,
,
∴![]() ,
,
∴PQ=3t,
故答案为:3t;
(2)当![]() 时,可列
时,可列![]() ,
,![]() ,符合题意
,符合题意
当![]() 时,可列
时,可列![]() ,
,![]() ,不符合题意,故舍去.
,不符合题意,故舍去.
综上,当![]() 的长度为10时,
的长度为10时,![]() 的值为
的值为![]() .
.
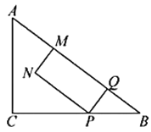
(3)如图1,当![]() 时,
时,![]() .
.
如图2,当![]() 时,
时,
 .
.


(4)如图,若NQ⊥AC,

∴NQ∥BC,
∴∠B=∠MQN,
∴tanB=tan∠MQN,
∴![]() ,
,
∴![]() =
=![]() ,
,
∴t=![]() ,
,
如图,若NQ⊥BC,

∴NQ∥AC,
∴∠A=∠BQN,
∴tanA=tan∠BQN,
∴![]() ,
,
∴![]() ,
,
∴t=![]()
综上所述:当t=![]() 或
或![]() 时,过点Q和点N的直线垂直于Rt△ABC的一边.
时,过点Q和点N的直线垂直于Rt△ABC的一边.

【题目】某市一研究机构为了了解![]() 岁年龄段市民对创建文明城市的关注程度,随机选取了
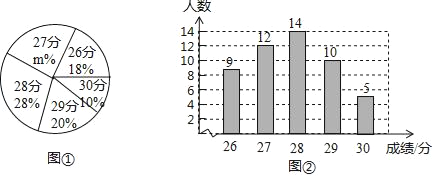
岁年龄段市民对创建文明城市的关注程度,随机选取了![]() 名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
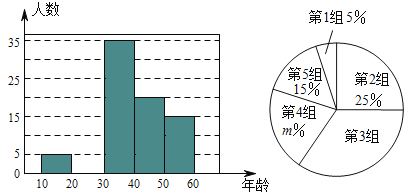
(1)请直接写出![]() ,第
,第![]() 组人数在扇形统计图中所对应的圆心角是 度;
组人数在扇形统计图中所对应的圆心角是 度;
(2)请补全上面的频数分布直方图:
(3)假设该市现有![]() 岁的市民
岁的市民![]() 万人,问
万人,问![]() 岁年龄段的关注创建文明城市的人数约有多少?
岁年龄段的关注创建文明城市的人数约有多少?