题目内容
1.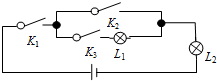 物理某一实验的电路图如图所示,其中K1,K2,K3 为电路开关,L1,L2为能正常发光的灯泡.任意闭合开关K1,K2,K3中的两个,那么能让两盏灯泡同时发光的概率为( )
物理某一实验的电路图如图所示,其中K1,K2,K3 为电路开关,L1,L2为能正常发光的灯泡.任意闭合开关K1,K2,K3中的两个,那么能让两盏灯泡同时发光的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与能让两盏灯泡同时发光的情况,再利用概率公式求解即可求得答案.
解答 解:画树状图得:
∵共有6种等可能的结果,能让两盏灯泡同时发光的有2种情况,
∴能让两盏灯泡同时发光的概率为:P=$\frac{2}{6}$=$\frac{1}{3}$.
故选A.
点评 本题考查了列表法与树状图法.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
11. 某市记者为了调查该市市民对雾霾天气成因的认识情况,进行了随机调查,并对结果绘制成如下不完整的统计图表.
某市记者为了调查该市市民对雾霾天气成因的认识情况,进行了随机调查,并对结果绘制成如下不完整的统计图表.
请根据图表中提供的信息解答下列问题:
(1)m=40,n%=15%;
(2)若该市人口约为60万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,抽中持C组“观点”的人概率是多少?
 某市记者为了调查该市市民对雾霾天气成因的认识情况,进行了随机调查,并对结果绘制成如下不完整的统计图表.
某市记者为了调查该市市民对雾霾天气成因的认识情况,进行了随机调查,并对结果绘制成如下不完整的统计图表.| 组别 | 观点 | 频数 |
| A | 大气气压低,空气不流动 | 80 |
| B | 地面灰尘大,空气湿度低 | m |
| C | 汽车尾气排放 | p |
| D | 工厂造成的污染 | 120 |
| E | 其他 | 60 |
(1)m=40,n%=15%;
(2)若该市人口约为60万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,抽中持C组“观点”的人概率是多少?
16.-2的绝对值是( )
| A. | ±2 | B. | 2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |




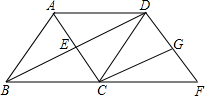 已知菱形ABCD的对角线AC与BD相交于点E,点F在BC的延长线上,且CF=BC,连接DF,点G是DF中点,连接CG.求证:四边形ECGD是矩形.
已知菱形ABCD的对角线AC与BD相交于点E,点F在BC的延长线上,且CF=BC,连接DF,点G是DF中点,连接CG.求证:四边形ECGD是矩形.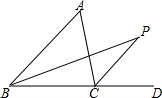 如图,△ABC的外角∠ACD的平分线与内角∠ABC平分线交于点P,若∠BPC=25°,则∠BAC的度数是50°.
如图,△ABC的外角∠ACD的平分线与内角∠ABC平分线交于点P,若∠BPC=25°,则∠BAC的度数是50°.