题目内容
3.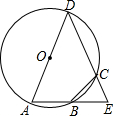 如图,以△ADE的边AD为直径的⊙O交AE于B,交DE于C,$\widehat{AB}$=$\widehat{BC}$,求证:BC=BE.
如图,以△ADE的边AD为直径的⊙O交AE于B,交DE于C,$\widehat{AB}$=$\widehat{BC}$,求证:BC=BE.
分析 连接BD,根据圆周角定理得到BD⊥AE,由$\widehat{AB}$=$\widehat{BC}$,得到∠ADB=∠EDB,推出△ADB≌△EDB,根据全等三角形的性质得到∠A=∠E,由圆内接四边形的性质得到∠BCE=∠A,等量代换得到∠BCE=∠E,即可得到结论.
解答  证明:连接BD,∵AD是⊙O的直径,
证明:连接BD,∵AD是⊙O的直径,
∴BD⊥AE,
∵$\widehat{AB}$=$\widehat{BC}$,
∴∠ADB=∠EDB,
在△ADB与△EDB中,$\left\{\begin{array}{l}{∠ADB=∠EDB}\\{BD=BD}\\{∠ABD=∠EBD=90°}\end{array}\right.$,
∴△ADB≌△EDB,
∴∠A=∠E,
∵∠BCE=∠A,
∴∠BCE=∠E,
∴BC=BE.
点评 本题考查了圆周角定理,全等三角形的判定和性质,圆内接四边形的性质,等腰三角形的判定.正确的作出辅助线是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
12.下列说法正确的是( )
| A. | 棱柱的各条棱都相等 | |
| B. | 有9条棱的棱柱的底面一定是三角形 | |
| C. | 长方体和正方体不是棱柱 | |
| D. | 柱体的上、下两底面可以大小不一样 |
 如图,OA表示北偏东40°方向的一条射线,仿照这条射线画出表示下列方向的射线:
如图,OA表示北偏东40°方向的一条射线,仿照这条射线画出表示下列方向的射线: