题目内容
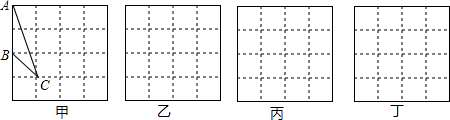
19．如图在4×4的方格纸（每小方格的面积为1）上有一个格点三角形ABC（图甲），（1）tanA=$\frac{1}{3}$；
（2）请在图乙、图丙、图丁中画出与三角形ABC相似（不全等）的格点三角形；
（3）图甲中的三角形和你画的图乙、图丙、图丁中的三角形的相似比分别是$\sqrt{2}$：1、$\sqrt{2}$：2、$\sqrt{2}$：$\sqrt{5}$．
分析 （1）利用图形结合锐角三角函数关系求出即可；
（2）根据三边对应成比例，两三角形相似分别作出三边之比为1：$\sqrt{2}$：$\sqrt{5}$的三角形即可；
（3）利用所画图形得出相似比即可．
解答 解：（1）如图甲所示：tanA=$\frac{1}{3}$．
故答案为：$\frac{1}{3}$；
（2）如图所示：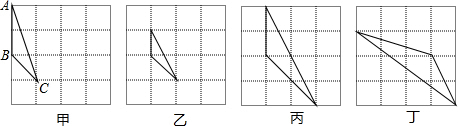
；
（3）图甲中的三角形和图乙、图丙、图丁中的三角形的相似比分别是：$\sqrt{2}$：1；$\sqrt{2}$：2，$\sqrt{2}$：$\sqrt{5}$．
故答案为：$\sqrt{2}$：1；$\sqrt{2}$：2，$\sqrt{2}$：$\sqrt{5}$．
点评 本题考查了利用相似变换作图以及锐角三角函数关系，利用网格结构确定出三角形的三边之比是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
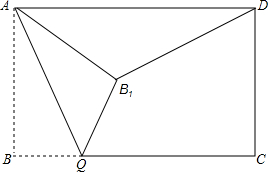如图，长方形ABCD中AB=2，BC=4，点Q是线段BC上一点，连接AQ，作点B关于直线AQ的对称点B，连接AB1，QB1．
如图，矩形ABCD中，AB=6，BC=$2\sqrt{3}$，点O是AB的中点，点P在AB的延长线上，且BP=3．一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速运动，到达A点后，立即以原速度沿AO返回；另一动点F从P点出发，以每秒1个单位长度的速度沿射线PA匀速运动，点E、F同时出发，当两点相遇时停止运动，在点E、F的运动过程中，以EF为边作等边△EFG，使△EFG和矩形ABCD在射线PA的同侧．设运动的时间为t秒（t≥0）．