题目内容
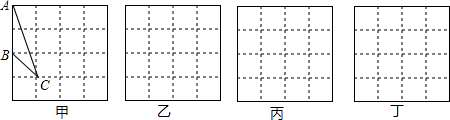
9.(1)如图1,在菱形ABCD中,∠ABC=60°,将一个足够大的直角三角板60°角的顶点E放在菱形ABCD的边BC上,其中三角板60°角的一边过点A,另一边与CD相交于点F.请判断线段AE、EF的数量关系,并说明理由;
(2)若将菱形换成正方形,把三角板的直角顶点E放在BC上,其中一条直角边经过点A,另一直角边与正方形ABCD的外角∠DCG的平分线相交于点F,
①把三角板的直角顶点E放在线段BC上(如图2),E是线段BC的中点,判断线段AE、EF的数量关系(直接写出结论).
②把三角板的直角顶点E移动到线段BC的延长线上(如图3),①中的结论是否成立?请说明理由.

分析 (1)在线段AB上截取BH=BE,连接EH,证明出AH=EC,∠ECF=∠AHE和∠FEC=∠BAE,利用ASA证明△AEH≌△ECF,即可得到AE=EF;
(2)取AB的中点M,点E是边BC的中点,根据条件利用ASA证明△AME≌△ECF,即可得到AE=EF;
(3)在线段BA的延长线上截取BH=BE,连接EH,依然利用ASA证明△AEH≌△ECF,即可得到AE=EF.
解答 解:(1)AE=EF,
理由:如图1.在线段AB上截取BH=BE,连接EH
∵四边形ABCD是菱形,
∴AB=BC,
∴AH=EC,
∵BH=BE,∠ABC=60°,
∴△BEH为等边三角形,
∴∠AHE=120°,
∵AB∥CD,∠ABC=60°,
∴∠ECF=120°,
∴∠ECF=∠AHE,
∵∠AEF+∠FEC=∠BAE+∠ABC,∠AEF=∠ABC=60°,
∴∠FEC=∠BAE,
在△AEH和△ECF中,
$\left\{\begin{array}{l}{∠AHE=∠ECF}\\{AH=EC}\\{∠BAE=∠FEC}\end{array}\right.$,
∴△AEH≌△ECF(ASA),
∴AE=EF;
(2)①AE=EF,
如图2,取AB的中点M,连接ME,
∵四边形ABCD是正方形
∴AB=BC,∠B=∠BCD=∠DCG=90°,
∵点E是边BC的中点,M是AB的中点,
∴AM=EC=BE,
∴∠BME=∠BEM=45°,
∴∠AME=135°,
∵CF平分∠DCG,
∴∠DCF=∠FCG=45°,
∴∠ECF=180°-∠FCG=135°,
∴∠AME=∠ECF,
∵∠AEF=90°,
∴∠AEB+∠CEF=90°,
又∵∠AEB+∠MAE=90°,
∴∠MAE=∠CEF,
在△AME和△ECF中,
$\left\{\begin{array}{l}{∠MAE=∠CEF}\\{AM=CE}\\{∠AME=∠ECF}\end{array}\right.$,
∴△AME≌△ECF(ASA),
∴AE=EF;
②成立.
理由:如图3,在线段BA的延长线上截取BH=BE,连接EH ,
,
∵四边形ABCD是正方形,
∴AB=BC,
∴AH=EC,
∵BH=BE,∠ABC=90°,
∴△BEH为等腰直角三角形,
∴∠AHE=45°,
∵CF平分∠DCG,
∴∠ECF=45°,
∴∠ECF=∠AHE,
∵∠AEF+∠FEC=∠BAE+∠ABC,∠AEF=∠ABC=90°,
∴∠FEC=∠BAE,
在△AEH和△ECF中,
$\left\{\begin{array}{l}{∠AHE=∠ECF}\\{AH=EC}\\{∠BAE=∠FEC}\end{array}\right.$,
∴△AEH≌△ECF(ASA),
∴AE=EF.
点评 此题主要考查了四边形综合题的知识,涉及到了正方形的性质、角平分线的性质及全等三角形的判定方法等知识,正确作出辅助线在BA延长线上截取AH=CE,构造三角形全等是解题关键,此题有一定的难度.

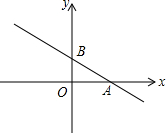 如图,已知直线y=-$\frac{1}{2}$x+1分别交x轴、y轴于A、B两点,点M在x轴上,且满足
如图,已知直线y=-$\frac{1}{2}$x+1分别交x轴、y轴于A、B两点,点M在x轴上,且满足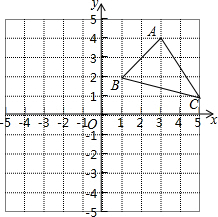 如图,在所给网格图(每小格边长均为1的正方形)中完成下列各题:
如图,在所给网格图(每小格边长均为1的正方形)中完成下列各题: