题目内容
14.已知x+y=$\sqrt{\sqrt{2015}+\sqrt{2014}}$,x-y=$\sqrt{\sqrt{2015}-\sqrt{2014}}$,则x4-y4=$\sqrt{2015}$.分析 把所给式子两边平方再相加可先求得x2+y2,再求得x2-y2,可求得答案.
解答 解:
∵x+y=$\sqrt{\sqrt{2015}+\sqrt{2014}}$,x-y=$\sqrt{\sqrt{2015}-\sqrt{2014}}$,
∴(x+y)2=x2+2xy+y2=($\sqrt{\sqrt{2015}+\sqrt{2014}}$)2=$\sqrt{2015}$+$\sqrt{2014}$,(x-y)2=x2-2xy+y2=($\sqrt{\sqrt{2015}-\sqrt{2014}}$)2=$\sqrt{2015}$-$\sqrt{2014}$,
∴x2+y2=$\sqrt{2015}$,
又x2-y2=(x+y)(x-y)=($\sqrt{\sqrt{2015}+\sqrt{2014}}$)($\sqrt{\sqrt{2015}-\sqrt{2014}}$)=$\sqrt{(\sqrt{2015})^{2}-(\sqrt{2014})^{2}}$=1,
∴x4-y4=(x2+y2)(x2-y2)=$\sqrt{2015}$,
故答案为:$\sqrt{2015}$.
点评 本题主要考查二次根式的化简,利用乘法公式分别求得x2+y2和x2-y2的值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.星期日上午小明骑车去姥姥家吃午饭.已知从小明家去姥姥家的路是上坡路,吃过午饭后,下午按原路返回,设小明从家出发后所用的时间为x(小时),骑车所走的路程为y(千米),则y与x的函数图象大致是( )
| A. | 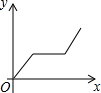 | B. | 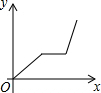 | C. | 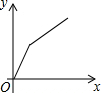 | D. | 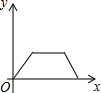 |
4.若分式$\frac{2x+y}{xy}$中,x、y的值都扩大3倍,则原分式的值( )
| A. | 扩大3倍 | B. | 缩小3倍 | C. | 不变 | D. | 无法确定 |
 如图,在△ABC中,∠ACB=90°,AB=10,cosB=$\frac{3}{5}$,G为BC上一点(不与B重合),以BG为直径的圆O交AB于D,作AD的垂直平分线交AD于F,交AC于E,连结DE.
如图,在△ABC中,∠ACB=90°,AB=10,cosB=$\frac{3}{5}$,G为BC上一点(不与B重合),以BG为直径的圆O交AB于D,作AD的垂直平分线交AD于F,交AC于E,连结DE.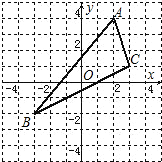 如图,△ABC中,A点坐标为(2,4),B点坐标为(-3,-2),C点坐标为(3,1).
如图,△ABC中,A点坐标为(2,4),B点坐标为(-3,-2),C点坐标为(3,1).