题目内容
已知PA是⊙O的切线,A为切点,PBC是割线,且AC是⊙O的直径,若PA=4,BC=6,则sin∠P的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:根据切割线定理求PB、PC,运用勾股定理求AC,运用三角函数的定义求解.
解答: 解:∵PA是⊙O的切线,A为切点,
解:∵PA是⊙O的切线,A为切点,
∴∠CAP=90°,
由切割线定理知,PA2=PB•PC=PB•(PB+BC),
∴PB=2,PC=8.
由勾股定理得,AC=4
,
sin∠P=
=
.
故选C.
 解:∵PA是⊙O的切线,A为切点,
解:∵PA是⊙O的切线,A为切点,∴∠CAP=90°,
由切割线定理知,PA2=PB•PC=PB•(PB+BC),
∴PB=2,PC=8.
由勾股定理得,AC=4
| 3 |
sin∠P=
| CA |
| PC |
| ||
| 2 |
故选C.
点评:本题考查了切割线定理、三角函数的定义.

练习册系列答案
相关题目
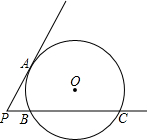 如图,已知PA是⊙O的切线,A为切点,PC与⊙O相交于B、C两点,PB=2cm,BC=8cm,则PA的长等于( )
如图,已知PA是⊙O的切线,A为切点,PC与⊙O相交于B、C两点,PB=2cm,BC=8cm,则PA的长等于( )| A、4cm | ||
| B、16cm | ||
| C、20cm | ||
D、2
|
已知PA是⊙O的切线,A为切点,PBC是过点O的割线,PA=10cm,PB=5cm,则⊙O的半径长为( )
| A、15cm | B、10cm | C、7.5cm | D、5cm |
 9、如图,已知PA是⊙O的切线,A是切点PC是过圆心的一条割线,点B、C是它与⊙O的交点,且PA=8,PB=4.则⊙O的半径为
9、如图,已知PA是⊙O的切线,A是切点PC是过圆心的一条割线,点B、C是它与⊙O的交点,且PA=8,PB=4.则⊙O的半径为 如图,已知PA是⊙O的切线,切点为A,PA=
如图,已知PA是⊙O的切线,切点为A,PA=