题目内容
在△ABC中，∠C=90°，cosA=
，则tanB的值为（ ）
| 1 |
| 2 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
考点：互余两角三角函数的关系
专题：
分析：根据互为余角两角的关系，可得sinB，根据特殊角三角函数值，可得答案．
解答：解：由△ABC中，∠C=90°，cosA=
，得
sinB=
．
由B是锐角，得
∠B=30°，
tanB=tan30°=
，
故选：C．
| 1 |
| 2 |
sinB=
| 1 |
| 2 |
由B是锐角，得
∠B=30°，
tanB=tan30°=
| ||
| 3 |
故选：C．
点评：本题考查了互为余角三角函数的关系，一个角的余弦等于它的余角的正弦．
练习册系列答案
相关题目
已知二次函数的图象（-3≤x≤0）如图所示．关于该函数在所给自变量取值范围内，下列说法正确的是（ ）| A、有最大值1，无最小值 |
| B、有最大值1，有最小值0 |
| C、有最大值1，有最小值-3 |
| D、有最大值0，有最小值-3 |
下列计算正确的是（ ）
| A、（x3）2=x5 | ||
| B、x2•x2=x5 | ||
| C、（-2x）3=-8x3 | ||
D、-2a2÷
|
在Rt△ABC中，∠C=90°，a、b、c分别是∠A、∠B、∠C的对边，下列等式中正确的是（ ）
A、cosA=
| ||
B、sinB=
| ||
C、tanB=
| ||
D、cotA=
|
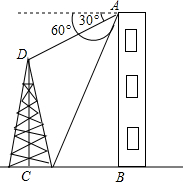如图，小明在300米高的楼顶上点A处测得一塔的塔顶D与塔基C的俯角分别为30°和60°，则塔高CD为（ ）| A、100米 | ||
B、100
| ||
| C、180米 | ||
| D、200米 |
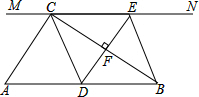如图，在Rt△ABC中，∠ACB=90°，过点C的直线MN∥AB，D在AB边上一点．过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE．