题目内容
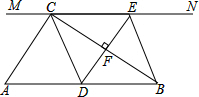 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D在AB边上一点.过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D在AB边上一点.过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.(1)求证:CE=AD;
(2)当点D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.
考点:菱形的判定,平行四边形的判定与性质
专题:
分析:(1)先求出四边形ADEC是平行四边形,根据平行四边形的性质推出即可;
(2)求出四边形BECD是平行四边形,求出CD=BD,根据菱形的判定推出即可;
(2)求出四边形BECD是平行四边形,求出CD=BD,根据菱形的判定推出即可;
解答:(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形;
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形;
点评:本题考查了平行四边形的性质和判定,菱形的判定,直角三角形的性质的应用,主要考查学生运用定理进行推理的能力.

练习册系列答案
相关题目
在△ABC中,∠C=90°,cosA=
,则tanB的值为( )
| 1 |
| 2 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
下列各点中,在第二象限的是( )
| A、(1,2) |
| B、(1,-2) |
| C、(0,2) |
| D、(-1,2) |
 如图是用围棋棋子在6×6的正方形网格中摆出的图案,棋子的位置用有序数对表示,如A点为(5,1),若再摆一黑一白两枚棋子,使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是( )
如图是用围棋棋子在6×6的正方形网格中摆出的图案,棋子的位置用有序数对表示,如A点为(5,1),若再摆一黑一白两枚棋子,使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是( )| A、黑(1,5),白(5,5) |
| B、黑(3,2),白(3,3) |
| C、黑(3,3),白(3,1) |
| D、黑(3,1),白(3,3) |
 如图,直线AB的解析式为y=2x-2,它与x轴,y轴分别交于A,B两点,若点P(a,b),Q(c,d)是直线AB上两动点,当点P,Q在直线AB上运动时.下列两个结论:①2a(2c-d)+b(2c-d)的值不变;②2a(d-2c)+b(2c-d)的值不变.判断哪个结论正确.并说明理由.
如图,直线AB的解析式为y=2x-2,它与x轴,y轴分别交于A,B两点,若点P(a,b),Q(c,d)是直线AB上两动点,当点P,Q在直线AB上运动时.下列两个结论:①2a(2c-d)+b(2c-d)的值不变;②2a(d-2c)+b(2c-d)的值不变.判断哪个结论正确.并说明理由.