题目内容
17.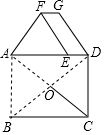 如图,在矩形ABCD中,AB=6,BC=8,AC和BD相交于点O,将△ABO绕点A逆时针旋转90°得到△AEF,将线段OD绕点D顺时针旋转90°得到△AEF,将线段OD绕点D顺时针旋转90°得到线段DG,则FG的长为( )
如图,在矩形ABCD中,AB=6,BC=8,AC和BD相交于点O,将△ABO绕点A逆时针旋转90°得到△AEF,将线段OD绕点D顺时针旋转90°得到△AEF,将线段OD绕点D顺时针旋转90°得到线段DG,则FG的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据矩形的性质得到AO=BO=OD,∠BAD=90°,于是得到∠ABO+∠ADO=90°,根据旋转的性质得到EF=OB,∠AEF=∠ABO,AE=AB=6,DG=OD,∠GDA+∠ADO=90°,等量代换得到∠AEF=∠ADG,根据平行线的判定得到FE∥DG,EF=DG,推出四边形EFGD是平行四边形,根据平行四边形的性质即可得到结论.
解答 解:∵四边形ABCD是矩形,
∴AO=BO=OD,∠BAD=90°,
∴∠ABO+∠ADO=90°,
∵将△ABO绕点A逆时针旋转90°得到△AEF,
∴EF=OB,∠AEF=∠ABO,AE=AB=6,
∵将线段OD绕点D顺时针旋转90°得到线段DG,
∴DG=OD,∠GDA+∠ADO=90°,
∴∠ABO=∠ADG,
∴∠AEF=∠ADG,
∴FE∥DG,EF=DG,
∴四边形EFGD是平行四边形,
∴FG=DE=AD-AE=8-6=2,
故选B.
点评 本题考查了矩形的性质平行四边形的判定和性质,旋转的性质,熟练掌握旋转的性质是解题的关键.

练习册系列答案
相关题目
8.正八边形的每一个内角的度数为( )
| A. | 45° | B. | 60° | C. | 120° | D. | 135° |
5.以下四个选项表示某天四个城市的平均气温,其中平均气温最低的是( )
| A. | -2 | B. | 5 | C. | -10 | D. | -5 |
12.若a与-2互为相反数,则a-1的值为( )
| A. | -3 | B. | -$\frac{3}{2}$ | C. | -$\frac{1}{2}$ | D. | 1 |
2.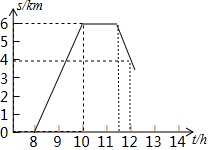 某班师生组织植树活动,上午8时从学校出发,到达植树地点后植树1.5h,然后按原路返回,如图为师生离校路程s(km)与时间t(h)之间的函数关系图象,则师生回到学校的时间为( )
某班师生组织植树活动,上午8时从学校出发,到达植树地点后植树1.5h,然后按原路返回,如图为师生离校路程s(km)与时间t(h)之间的函数关系图象,则师生回到学校的时间为( )
 某班师生组织植树活动,上午8时从学校出发,到达植树地点后植树1.5h,然后按原路返回,如图为师生离校路程s(km)与时间t(h)之间的函数关系图象,则师生回到学校的时间为( )
某班师生组织植树活动,上午8时从学校出发,到达植树地点后植树1.5h,然后按原路返回,如图为师生离校路程s(km)与时间t(h)之间的函数关系图象,则师生回到学校的时间为( )| A. | 12时30分 | B. | 12时45分 | C. | 13时 | D. | 13时30分 |
9.若代数式$\frac{1}{x+3}$在实数范围内有意义,则实数x的取值范围是( )
| A. | x=-3 | B. | x≠-3 | C. | x<-3 | D. | x>-3 |
7.若a<b,则下列各式中一定正确的是( )
| A. | -a>-b | B. | a-b>0 | C. | a+3>b+3 | D. | ac<bc |
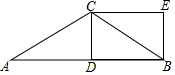 如图,在△ABC中,AC=BC,CD平分∠ACB交AB于D,CE∥AB,且CE=$\frac{1}{2}$AB.
如图,在△ABC中,AC=BC,CD平分∠ACB交AB于D,CE∥AB,且CE=$\frac{1}{2}$AB.