题目内容
16.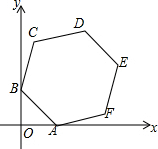 如图,正六边形ABCDEF的边长为4,两顶点A,B分别在x轴和y轴上运动,则顶点D到原点O的距离的最大值为2+2$\sqrt{13}$;最小值为2$\sqrt{13}$-2.
如图,正六边形ABCDEF的边长为4,两顶点A,B分别在x轴和y轴上运动,则顶点D到原点O的距离的最大值为2+2$\sqrt{13}$;最小值为2$\sqrt{13}$-2.
分析 根据已知得出D点的两个特殊位置,进而求出即可.
解答 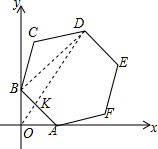 解:当O、D、AB中点共线时,OD有最大值和最小值,
解:当O、D、AB中点共线时,OD有最大值和最小值,
如图,BD=4$\sqrt{3}$,BK=2,
∴DK=$\sqrt{B{D}^{2}+B{K}^{2}}$=$\sqrt{52}$=2$\sqrt{13}$,OK=BK=2,
∴OD的最大值为:2+2$\sqrt{13}$,
同理,当O、D、AB中点共线时,将正六边形绕AB中点K旋转180°取得最小值为:2$\sqrt{13}$-2,
故答案为:2+2$\sqrt{13}$,2$\sqrt{13}$-2.
点评 此题主要考查了正多边形的性质以及坐标轴的几何变换,做此类问题时,要先由特殊点考虑进行计算.

练习册系列答案
相关题目
7.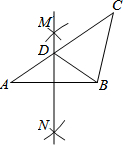 如图,在△ABC中,按以下步骤作图:①分别以点A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠C=44°,则∠A等于( )
如图,在△ABC中,按以下步骤作图:①分别以点A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠C=44°,则∠A等于( )
 如图,在△ABC中,按以下步骤作图:①分别以点A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠C=44°,则∠A等于( )
如图,在△ABC中,按以下步骤作图:①分别以点A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠C=44°,则∠A等于( )| A. | 35° | B. | 34° | C. | 32° | D. | 30° |
11.已知一次函数y=-2x+4的图象经过点(x1,y1),(x2,y2),且y1<y2,则有( )
| A. | x1>x2 | B. | x1=x2 | C. | x1<x2 | D. | 无法确定 |
8.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5.在下列图形中,中心对称图形是( )
| A. | 等边三角形 | B. | 平行四边形 | C. | 等腰梯形 | D. | 正五边形 |
 如图,数轴上的点P表示的数是-1,将点P向右移动3个单位长度得到点P′,则点P′表示的数是2;数轴上到原点的距离等于2的点所表示的数是-2和2.
如图,数轴上的点P表示的数是-1,将点P向右移动3个单位长度得到点P′,则点P′表示的数是2;数轴上到原点的距离等于2的点所表示的数是-2和2.