题目内容
19.在平面直角坐标系中,直线y=kx+b(k≠0)向上平移2个单位后与直线y=x重合,且直线y=kx+b(k≠0)与x轴交于点A,与y轴交于点B.(1)写出点B的坐标,求直线AB的表达式;
(2)求△AOB的面积.
分析 (1)根据平移得出直线的解析式,进而解答即可;
(2)根据三角形的面积公式解答即可.
解答 解:(1)因为直线y=kx+b(k≠0)向上平移2个单位后与直线y=x重合,
所以直线的解析式为:y=x-2,
把x=0代入y=x-2=-2,点B坐标为(0,-2)
把y=0代入0=x-2,解得:x=2,点A坐标为(2,0),
所以直线AB的解析式为:y=x-2;
(2)△AOB的面积=$\frac{1}{2}$×2×2=2.
点评 本题考查了一次函数与几何变换问题,关键是根据一次函数图象上点的坐标特征:一次函数y=kx+b(k≠0)的图象上的点满足其解析式解答.

练习册系列答案
相关题目
7.在?ABCD中,对角线AC和BD相交于点O,若AC=8,BD=6,则AB的长不可能是( )
| A. | 1 | B. | 2 | C. | 5 | D. | 6 |
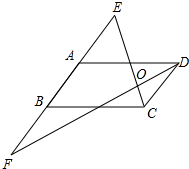 如图所示,在?ABCD中,2AB=AD,AB=AE=BF,求证:EC⊥DF.
如图所示,在?ABCD中,2AB=AD,AB=AE=BF,求证:EC⊥DF.