题目内容
2．
如图，在矩形ABCD中，AB=6cm，BC=8cm．点P由点A出发，沿AB边以1cm/s的速度向点B移动，点Q由点B出发，沿BC边以2cm/s的速度向点C移动．如果点P，Q同时出发，经过2或4秒后，△PBQ的面积等于8cm2．
分析 设t秒钟后，S△PBQ=8，则AP=t，PB=AB-AP=6-t，QB=2t，而S△PBQ=$\frac{1}{2}$PB×QB，由此可以列出方程求解．
解答 解：设t秒钟后，S△PBQ=8，
则$\frac{1}{2}$×2t（6-t）=8，
t2-6t+8=0，
解得t1=2，t2=4，
答：2或4秒后△PBQ的面积等于8cm2．
故答案为2或4．
点评 本题考查一元二次方程的应用，解题需准确找到两个直角三角形的两条直角边的代数值，然后根据三角形的面积公式列出方程解题．
练习册系列答案
同步练习强化拓展系列答案
相关题目
13．若点P（3，2m-1）在第四象限，则m的取值范围是（ ）
| A． | m＞$\frac{1}{2}$ | B． | m＜$\frac{1}{2}$ | C． | m≥-$\frac{1}{2}$ | D． | m≤$\frac{1}{2}$ |
17．
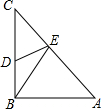如图，在Rt△ABC中，AB=BC=4，D到为BC的中点，AC边上存在一点E，则△BDE周长的最小值为（ ）
如图，在Rt△ABC中，AB=BC=4，D到为BC的中点，AC边上存在一点E，则△BDE周长的最小值为（ ）| A． | $2\sqrt{5}$ | B． | $2\sqrt{3}$ | C． | $2\sqrt{5}+2$ | D． | $2\sqrt{3}+2$ |
7．下列说法：①35=3×3×3×3×3；②-1是单项式，且它的次数为1；③若∠1=90°-∠2，则∠1与∠2互为余角；④对于有理数n、x、y（其中xy≠0），若$\frac{n}{x}$=$\frac{n}{y}$，则x=y．其中不正确的有（ ）
| A． | 3个 | B． | 2个 | C． | 1个 | D． | 0个 |
14．下列分解因式正确的是（ ）
| A． | x2+2x+1=x（x+2）+1 | B． | （x2-4）x=x3-4x | C． | ax+bx=（a+b）x | D． | m2-2mn+n2=（m-n）2 |
如图，AB切⊙O于点A，且交直径EC的延长线于B，∠CAD=∠B，AB=$\frac{15}{4}$，BC=$\frac{5}{4}$，求弦CD的长．