题目内容
11. 如图,AB切⊙O于点A,且交直径EC的延长线于B,∠CAD=∠B,AB=$\frac{15}{4}$,BC=$\frac{5}{4}$,求弦CD的长.
如图,AB切⊙O于点A,且交直径EC的延长线于B,∠CAD=∠B,AB=$\frac{15}{4}$,BC=$\frac{5}{4}$,求弦CD的长.
分析 连接AE,CD,根据切割线定理得到AB2=BC•BE,求得BE=$\frac{45}{4}$,CE=BE-BC=10,根据相似三角形的性质得到$\frac{AE}{AC}$=$\frac{BE}{AB}$=3,设AE=3k,AC=k,根据勾股定理得到AC=$\sqrt{10}$,根据相似三角形的性质即可得到结论.
解答 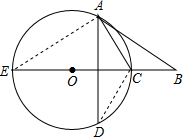 解:连接AE,CD,
解:连接AE,CD,
∵AB切⊙O于点A,
∴AB2=BC•BE,
∵AB=$\frac{15}{4}$,BC=$\frac{5}{4}$,
∴BE=$\frac{45}{4}$,
∴CE=BE-BC=10,
∵∠E=∠BAC,∠B=∠B,
∴△ABE∽△CBA,
∴$\frac{AE}{AC}$=$\frac{BE}{AB}$=3,
设AE=3k,AC=k,
∵CE是⊙O的直径,
∴∠EAC=90°,
∴AE2+AC2=CE2,
∴AC=$\sqrt{10}$,
∵∠CAD=∠B,∠D=∠CAB,
∴△ACD∽△BCA,
∴$\frac{AC}{BC}=\frac{CD}{AC}$,
即$\frac{\sqrt{10}}{\frac{5}{4}}$=$\frac{CD}{\sqrt{10}}$,
∴CD=8.
点评 本题考查了相似三角形的判定和性质,切线的性质,圆周角定理,勾股定理,正确的作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列计算正确的是( )
| A. | 2a+3b=6ab | B. | 19a2b2-9ab=10ab | C. | -2x2-2x2=0 | D. | 5y-3y=2y |
16.一个容量为40的样本最大值为35,最小值为12,取组距为4,则可以分为( )
| A. | 4组 | B. | 5组 | C. | 6组 | D. | 7组 |
3.已知m+n=3,则m2+2mn+n2-6的值( )
| A. | 12 | B. | 6 | C. | 3 | D. | 0 |
20.下列各组线段中不是成比例线段的是( )
| A. | 3m、4m、5m、6m | B. | 1cm、5cm、0.8cm、4cm | ||
| C. | 2.4m、1.5m、1.2m、0.75m | D. | 2cm、3cm、4cm、6cm |
 如图,在矩形ABCD中,AB=6cm,BC=8cm.点P由点A出发,沿AB边以1cm/s的速度向点B移动,点Q由点B出发,沿BC边以2cm/s的速度向点C移动.如果点P,Q同时出发,经过2或4秒后,△PBQ的面积等于8cm2.
如图,在矩形ABCD中,AB=6cm,BC=8cm.点P由点A出发,沿AB边以1cm/s的速度向点B移动,点Q由点B出发,沿BC边以2cm/s的速度向点C移动.如果点P,Q同时出发,经过2或4秒后,△PBQ的面积等于8cm2.