题目内容
如图，有三种卡片，其中边长为a的正方形卡片1张，长、宽分别为a、b的正方形4张，边长为b的正方形卡片4张，若用这9张卡片拼成一个正方形，求该正方形的面积．考点：完全平方公式的几何背景
专题：
分析：1张边长为a的正方形卡片的面积为a2，4张边长分别为a、b的矩形卡片的面积为4ab，4张边长为b的正方形卡片面积为4b2，9张卡片拼成一个正方形的总面积=a2+4ab+4b2=（a+2b）2，所以该正方形的面积：（a+2b）2．
解答：解：设拼成后大正方形的边长为x，
∴a2+4ab+4b2=x2，
∴（a+2b）2=x2，
∴该正方形的面积：（a+2b）2
∴a2+4ab+4b2=x2，
∴（a+2b）2=x2，
∴该正方形的面积：（a+2b）2
点评：本题主要考查了完全平方公式的几何背景，利用完全平方公式分解因式后即可得出大正方形的边长．
练习册系列答案
相关题目
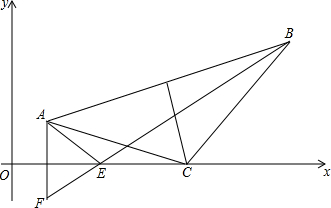如图，x轴是西气东输工程天然气的主管道，按规定主管道在我市只允许开一个口，A（2，1），B（10，5）是我市新建的两个天然气站，现在要在x轴上选一个点开口，分别连接到A、B，小明说：“作AB的垂直平分线交x轴于C，就选点C，C点到A、B的距离相等．“小华说：“不行，可以用轴对称知识做出点E，点E到A、B的距离之和最小，这样可以节约原材料，节省费用．“请你求出：