题目内容
根据某种规律观察下列式子:
1+2=3,4+5+6=7+8,9+10+11+12=13+14+15,定义以上各式的“计算结果”分别是3,15,42…那么含有数2003算式的“计算结果”为 .
1+2=3,4+5+6=7+8,9+10+11+12=13+14+15,定义以上各式的“计算结果”分别是3,15,42…那么含有数2003算式的“计算结果”为
考点:规律型:数字的变化类
专题:
分析:第一个式子3个数字,第二个式子5个数字,以后分别是7、9…即第n个式子有2n+1个数字.因此有2003个数字的是第
(2003-1)=1001个式子.第1001个式子的加数就因此从2002999开始,等号前加数共有1002个,等号后加数共有1001个,由此进一步计算得出答案即可.
| 1 |
| 2 |
解答:解:由题意可知第n个式子有2n+1个数字.
因此有2003个数字的是第
(2003-1)=1001个式子.
第1001个式子,前面的式子数字个数从3、5、7、…到2001个.
一共有
(3+2001)(2001-3+1)=2002998,
第1001个式子的加数就因此从2002999开始,
等号前加数共有1002个,等号后加数共有1001个
2002999+1002-1=2004000,
2004001+1001-1=2005001,
这个式子就是:
2002999+2003000+2003001+…+2004000=2004001+2004002+2004003+…+2005001.
因此有2003个数字的是第
| 1 |
| 2 |
第1001个式子,前面的式子数字个数从3、5、7、…到2001个.
一共有
| 1 |
| 2 |
第1001个式子的加数就因此从2002999开始,
等号前加数共有1002个,等号后加数共有1001个
2002999+1002-1=2004000,
2004001+1001-1=2005001,
这个式子就是:
2002999+2003000+2003001+…+2004000=2004001+2004002+2004003+…+2005001.
点评:此题考查数字的变化规律,从简单的算式中找出规律,利用规律解决问题.

练习册系列答案
相关题目
大于-4且小于5的整数一共有( )
| A、6个 | B、7个 | C、8个 | D、9个 |
 已知点A的坐标为(3,1),⊙A与坐标轴有三个公共点.在如图所示的平面直角坐标系中画出⊙A,并求⊙A的半径.
已知点A的坐标为(3,1),⊙A与坐标轴有三个公共点.在如图所示的平面直角坐标系中画出⊙A,并求⊙A的半径.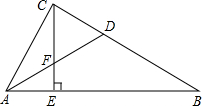 如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,CE⊥AB,垂足为E,交AD于点F,试猜想△CFD的形状,证明你的结论.
如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,CE⊥AB,垂足为E,交AD于点F,试猜想△CFD的形状,证明你的结论. 如图,有三种卡片,其中边长为a的正方形卡片1张,长、宽分别为a、b的正方形4张,边长为b的正方形卡片4张,若用这9张卡片拼成一个正方形,求该正方形的面积.
如图,有三种卡片,其中边长为a的正方形卡片1张,长、宽分别为a、b的正方形4张,边长为b的正方形卡片4张,若用这9张卡片拼成一个正方形,求该正方形的面积. 已知D是AB上的一点,
已知D是AB上的一点, 如图所示,已知AB=AC,∠B=∠C,BE=CD,则图中共有全等三角形
如图所示,已知AB=AC,∠B=∠C,BE=CD,则图中共有全等三角形