题目内容
如图，有理数a，b在数轴上的位置如图所示：
则在a+b，b-2a，|b|-|a|，|a-b|，|a+2|，-|b-4|中负数共有（ ）
则在a+b，b-2a，|b|-|a|，|a-b|，|a+2|，-|b-4|中负数共有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
考点：数轴,正数和负数
专题：
分析：根据数轴上的数，右边的数总是大于左边的数，即可得到a，b的大小关系，再利用有理数的运算法则以及绝对值的性质分别进行判断．
解答：解：∵有理数a、b在数轴上的位置如图所示，
∴-2＜a＜-1，0＜b＜1，
∴a+b＜0；
b-2a＞0；
|b|-|a|=b+a＜0；
|a-b|=-a+b＞0；
|a+2|=a+2＞0；
-|b-4|＜0．
∴在a+b，b-2a，|b|-|a|，|a-b|，|a+2|，-|b-4|中负数共有3个．
故选：C．
∴-2＜a＜-1，0＜b＜1，
∴a+b＜0；
b-2a＞0；
|b|-|a|=b+a＜0；
|a-b|=-a+b＞0；
|a+2|=a+2＞0；
-|b-4|＜0．
∴在a+b，b-2a，|b|-|a|，|a-b|，|a+2|，-|b-4|中负数共有3个．
故选：C．
点评：此题主要考查了绝对值的性质以及数轴上的数：右边的数总是大于左边的数，从而确定a，b的大小关系，并且考查了有理数的运算法则．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
用网格中所给形状的纸片，只能折叠成一个无盖纸盒，为使纸盒有“盖“，需在图中再选画出一个小正方形．请你在图中把所有可能情况都指出来（在可选的小方格内依次填写一个数字）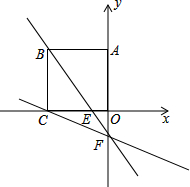
已知，如图，四边形OABC是边长为3的正方形，其中O为坐标原点，点A在y轴的正半轴上，点C在x轴的负半轴上，直线y=-
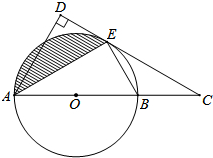如图，已知AB为⊙O的直径，C是AB延长线上一点，CD与⊙O相切于点E，AD⊥CD，垂足为D．