题目内容
20.计算:(1)($\frac{1}{3}$)-3-(3.4-π)0+(-2)4
(2)m•m2•m3+(-2m3)2-m8÷m2
(3)(x+2y)2(x-2y)2
(4)(a-3b-2c)(a-3b+2c)
分析 (1)先算负整数指数幂,零指数幂,乘方,再相加减即可求解;
(2)先算同底数幂的乘法,积的乘方,同底数幂的除法,再合并同类项即可求解;
(3)先根据平方差公式计算,再根据完全平方公式计算;
(4)先根据平方差公式计算,再根据完全平方公式计算.
解答 解:(1)($\frac{1}{3}$)-3-(3.4-π)0+(-2)4
=27-1+16
=42;
(2)m•m2•m3+(-2m3)2-m8÷m2
=m6+4m6-m6
=4m6;
(3)(x+2y)2(x-2y)2
=(x2-4y2)2
=x4-8x2y2+16y4;
(4)(a-3b-2c)(a-3b+2c)
=(a-3b)2-(2c)2
=a2-6ab+9b2-4c2.
点评 考查了整式的混合运算.
(1)有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.
(2)“整体”思想在整式运算中较为常见,适时采用整体思想可使问题简单化,并且迅速地解决相关问题,此时应注意被看做整体的代数式通常要用括号括起来.

练习册系列答案
相关题目
10.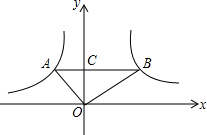 如图,在直角坐标系中,O为坐标原点,函数y1=$\frac{{k}_{1}}{x}$(x<0)和y2=$\frac{{k}_{2}}{x}$(x>0)的图象上,分别有A、B两点,若AB∥x轴且交y轴于点C,且OA⊥OB,S△AOC=$\frac{1}{2}$,S△BOC=$\frac{9}{2}$,则线段AB的长度为( )
如图,在直角坐标系中,O为坐标原点,函数y1=$\frac{{k}_{1}}{x}$(x<0)和y2=$\frac{{k}_{2}}{x}$(x>0)的图象上,分别有A、B两点,若AB∥x轴且交y轴于点C,且OA⊥OB,S△AOC=$\frac{1}{2}$,S△BOC=$\frac{9}{2}$,则线段AB的长度为( )
 如图,在直角坐标系中,O为坐标原点,函数y1=$\frac{{k}_{1}}{x}$(x<0)和y2=$\frac{{k}_{2}}{x}$(x>0)的图象上,分别有A、B两点,若AB∥x轴且交y轴于点C,且OA⊥OB,S△AOC=$\frac{1}{2}$,S△BOC=$\frac{9}{2}$,则线段AB的长度为( )
如图,在直角坐标系中,O为坐标原点,函数y1=$\frac{{k}_{1}}{x}$(x<0)和y2=$\frac{{k}_{2}}{x}$(x>0)的图象上,分别有A、B两点,若AB∥x轴且交y轴于点C,且OA⊥OB,S△AOC=$\frac{1}{2}$,S△BOC=$\frac{9}{2}$,则线段AB的长度为( )| A. | 3$\sqrt{3}$ | B. | $\frac{10}{3}$$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 4 |
8.多项式4x2+mxy+25y2是完全平方式,则m的值是( )
| A. | 20 | B. | 10 | C. | 10或-10 | D. | 20或-20 |
5.下列说法正确的是( )
| A. | 2x+y=3的解也是方程组$\left\{{\begin{array}{l}{2x+y=3}\\{x-3y=5}\end{array}}\right.$的解 | |
| B. | x-3y=5的解也是方程组$\left\{{\begin{array}{l}{2x+y=3}\\{x-3y=5}\end{array}}\right.$的解 | |
| C. | 方程组$\left\{{\begin{array}{l}{2x+y=3}\\{x-3y=5}\end{array}}\right.$的解是2x+y=3和x-3y=5的解 | |
| D. | 2x+y=3有无数个正整数解 |
12.计算下列各式,结果是x8的是( )
| A. | x2•x4 | B. | (x2)6 | C. | x4+x4 | D. | x4•x4 |