题目内容
2.先化简再求值:(x2-xy)÷$\frac{{x}^{2}-2xy{+y}^{2}}{xy}$•$\frac{{x}^{2}{-y}^{2}}{{x}^{2}}$,其中|x-2|+y2-6y=-9.分析 先把分子分母因式分解,再把除法运算化为乘法运算,然后约分得到原式=xy+y2,再利用非负数的性质得到x和y的值,最后把x、y的值代入原式=xy+y2中计算即可.
解答 解:原式=x(x-y)•$\frac{xy}{(x-y)^{2}}$•$\frac{(x+y)(x-y)}{{x}^{2}}$
=y(x+y)
=xy+y2,
∵|x-2|+y2-6y=-9,
∴|x-2|+(y-3)2=0,
∴x-2=0,y-3=0,解得x=2,y=3,
∴原式=2×3+32=15.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也考查了非负数的性质.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
7.下列各式可用完全平方公式计算的是( )
| A. | (2a-3b)(3b-2a) | B. | (2a-3b)(-3b+2a) | C. | (-2m+n)(2m+n) | D. | (2m+n)(2n-m) |
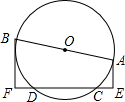 如图,AB是⊙O的直值,CD为弦,AE⊥CD于E,BF⊥CD于F.
如图,AB是⊙O的直值,CD为弦,AE⊥CD于E,BF⊥CD于F.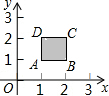 有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A(1,1)、B(2,1)、C(2,2)、D(1,2),用信号枪沿直线y=2x+b发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围为-3≤b≤0.
有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A(1,1)、B(2,1)、C(2,2)、D(1,2),用信号枪沿直线y=2x+b发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围为-3≤b≤0.