题目内容
18．下列命题：①矩形的对角线互相平分；②一组对边和一组对角相等的四边形是平行四边形；③连接矩形四边中点所得的四边形是菱形；④对角线互相垂直平分且相等的四边形是正方形．其中的真命题是（ ）| A． | ①②③ | B． | ①②④ | C． | ①③④ | D． | ①②③④ |
分析 利用矩形的性质以及中点四边形的判定方法和正方形的判定方法分别分析得出答案．
解答 解：：①矩形的对角线互相平分，正确；
②一组对边和一组对角相等的四边形是平行四边形，错误，
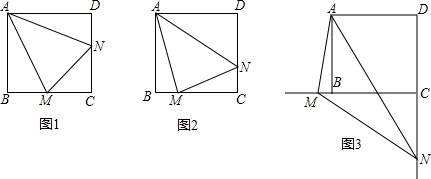
如图所示：
AB=CD，∠B=∠D，AC=AC，
无法得出△ABC≌△ADC，
∴BC不一定等于AD，
∴四边形ABCD不一定是平行四边形，
∴一组对边相等且一组对角相等的四边形不一定是平行四边形，故此选项错误；
③连接矩形四边中点所得的四边形是菱形，正确；
④对角线互相垂直平分且相等的四边形是正方形，正确．
故选；C．
点评 此题主要考查了命题与定理，正确把握平行四边形的判定方法是解题关键．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
如图，在四边形ABCD中，∠A=90°，AD∥BC，E为AB的中点，连接CE，BD，过点E作FE⊥CE于点E，交AD于点F，连接CF，已知2AD=AB=BC．
13．下列方程中，是一元二次方程的是（ ）
| A． | 4x2=3y | B． | x（x+1）=5x2-1 | C． | $\sqrt{x}$-3=5x2-$\sqrt{6}$ | D． | $\frac{1}{{x}^{2}}$+3x-1=0 |
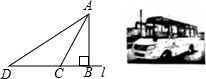如图是我市投入使用的“大鼻子”校车，其安全隐患主要是超速和超载，某中学九年级数学活动小组设计了如下检测公路上行驶汽车速度的实验，先在笔直的车道l旁边选取一点A，再在l上确定点B，使AB⊥l，测得AB的长为30米，又在l上选取点C，D，使∠CAB=30°，∠DAB=60°，如图所示．