题目内容
如图1,已知△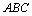 中,
中,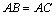 ,现在△
,现在△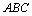 外作∠
外作∠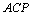 =∠
=∠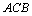 ,在
,在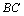 上取一点
上取一点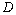 ,在
,在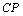 上取一点
上取一点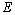 ,使
,使 ,并连接
,并连接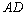 ,
,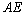 .
.
(1)求证: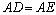 ;
;
(2)若∠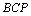 =144°,求∠
=144°,求∠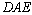 的度数;
的度数;
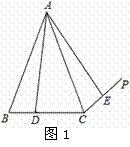
(3)如图2,若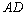 ⊥
⊥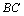
 ,过点
,过点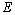 作
作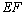 ∥
∥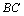 交
交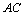 于点
于点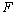 ,连接
,连接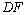
 .试判断四边形
.试判断四边形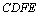 的形状,并给出证明.
的形状,并给出证明.

证明:(1)∵AB=AC,∴∠B=∠ACB,又∵∠ACP=∠ACB,∴∠B=∠ACP,
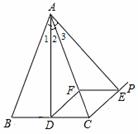
在△ABD和△ACE中,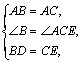 ∴△ABD
∴△ABD ≌△ACE,∴AD=AE;
≌△ACE,∴AD=AE;
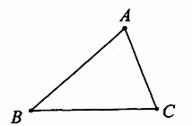
(2)∵∠B=∠ACB=∠ACP,∠BCP=144°,∴∠B=∠ACB=∠ACP=72°,
 ∴∠BAC=36°,
∴∠BAC=36°,
由(1)知,△ABD≌△ACE,∴∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,即∠DAE=∠BAC=36°. ………………8分
(3)四边形CDFE 为菱形.理由如下:
∵AB=AC,AD⊥BC,∴BD=CD,∠1=∠2,
又∵BD=CE,∴CE=CD,
由(1)知,△ABD≌△ACE,
∴∠1=∠3,∴∠2=∠3,
在△ADF和△AEF中, ∴△ADF≌△AEF,∴DF=EF,
∴△ADF≌△AEF,∴DF=EF,
∵EF∥BC,∴∠EFC=∠DCF,∴∠EFC=∠ECF,∴EC=EF,∴CD=CE=EF=DF,
∴四边形CDFE为菱形.
(注:利用其他方法证明,只要正确即可) 分

练习册系列答案
相关题目
 ,运动时间为
,运动时间为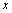 ,则下列图象中能大致表示
,则下列图象中能大致表示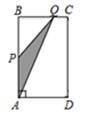
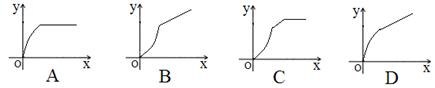
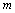 ,
, )表示第
)表示第
 并简要说明理由.
并简要说明理由.

 __________.
__________. )
)