题目内容
如图,在正方形ABCD中,等边三角形DEF的顶点E、F分别在AB和BC上。
(1)求证:BE=BF;
(2)若等边三角形DEF的边长为2,求正方形ABCD的周长。

(1)证明:∵四边形ABCD是正方形,
∴ AB=BC=CD=DA , ∠A=∠B=∠C=90°
∵△DEF是等边三角形,
∴DE=DF
∴Rt△ADE≌Rt△CDF(HL)………………………………………………2分
∴AE=CF
∴AB-AE=BC-CF
即 BE=BF…………………………………………………………4分
(2)设正方形ABCD的边长为a ,由(1)知BE=BF
又∠B=90°
∴BE2+BF2=EF2
即 2BE2=22 ∴BE=
∴ AE=AB-BE=a- …………………………………………6分
…………………………………………6分
在Rt△ADE中
AD2+AE2=DE2 即a2+(a- )2=22
)2=22
解得 a= (舍去负值) …………………………………………8分
(舍去负值) …………………………………………8分
∴正方形ABCD的周长= ×4=2(
×4=2( )=2
)=2 +2
+2 ………………9分
………………9分

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
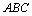 中,
中,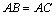 ,现在△
,现在△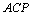 =∠
=∠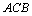 ,在
,在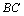 上取一点
上取一点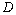 ,在
,在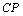 上取一点
上取一点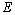 ,使
,使 ,并连接
,并连接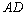 ,
,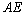 .
.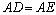 ;
;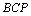 =144°,求∠
=144°,求∠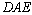 的度数;
的度数; ,过点
,过点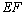 ∥
∥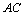 于点
于点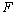 ,连接
,连接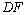
 .试判断四边形
.试判断四边形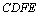 的形状,并给出证明.
的形状,并给出证明.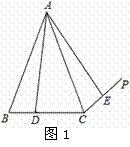

 = .
= . (k≠0)与一次函数y=x的图象有交点,则k的范围是______.
(k≠0)与一次函数y=x的图象有交点,则k的范围是______. 31 D.极差是5
31 D.极差是5 47°, 那么BC与DE平行吗?AB与CD呢?为什么?(8分)
47°, 那么BC与DE平行吗?AB与CD呢?为什么?(8分)