题目内容
已知关于x的一元二次方程x2﹣(2k+1)x+k2+2k=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)是否存在实数k使得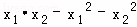 ≥0成立?若存在,请求出k的值;若不存在,请说明理由.
≥0成立?若存在,请求出k的值;若不存在,请说明理由.
解:(1)∵原方程有两个实数根,
∴[﹣(2k+1)]2﹣4(k2+2k)≥0,
∴4k2+4k+1﹣4k2﹣8k≥0
∴1﹣4k≥0,
∴k≤.
∴当k≤时,原方程有两个实数根.
(2)假设存在实数k使得 ≥0成立.
≥0成立.
∵x1,x2是原方程的两根,
∴ .
.
由 ≥0,
≥0,
得 ≥0.
≥0.
∴3(k2+2k)﹣(2k+1)2≥0,整理得:﹣(k﹣1)2≥0,
∴只有当k=1时,上式才能成立. 
又∵由(1)知k≤,
∴不存在实数k使得 ≥0成立.[来
≥0成立.[来

练习册系列答案
相关题目
某超市一月份的营业额为36万元,三月份的营 业额为48万元,设每月的平均增长率为x,则可列方程为( )
业额为48万元,设每月的平均增长率为x,则可列方程为( )
|
| A. | 48(1﹣x)2=36 | B. | 48(1+x)2=36 | C. | 36(1﹣x)2=48 | D. | 36(1+x)2=48 |
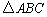 ,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线Ax上运动,当AP= 时,才能使△ABC与△PQA全等。
,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线Ax上运动,当AP= 时,才能使△ABC与△PQA全等。
 的两实数根分为
的两实数根分为 和
和 ,则
,则 。
。 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高是 cm.
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高是 cm.
 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线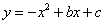 过A、B两点。(1)求这个抛物线的解析式;
过A、B两点。(1)求这个抛物线的解析式;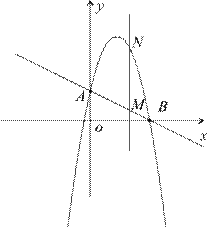
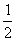 x(x-1)=240
x(x-1)=240
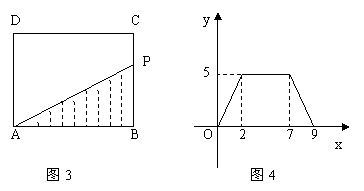
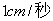 速度出发,沿BC、CD、DA运动到A点停止,设点P运动时间为
速度出发,沿BC、CD、DA运动到A点停止,设点P运动时间为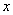 秒,
秒,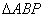 面积为
面积为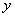
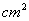 ,
,