题目内容
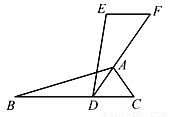
如图，已知△ABC≌△EDF，点F，A，D在同一条直线上，AD是∠BAC的平分线，∠EDA＝20°，∠F＝60°，则∠DAC的度数是（ ）
A. 50° B. 60° C. 100° D. 120°
A 【解析】根据全等三角形的性质求出∠B=∠EDF=20°和∠C=∠F =60°，根据三角形内角和定理求出∠BAC=180°﹣∠B﹣∠C=100°，根据角平分线定义求出∠DAC=∠BAC=50°， 故选：A．
练习册系列答案
名校课堂系列答案
相关题目
下表给出了代数式﹣x2+bx+c与x的一些对应值：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
﹣x2+bx+c | … | 5 | n | c | 2 | ﹣3 | ﹣10 | … |
（1）根据表格中的数据，确定b，c，n的值；
（2）设y=﹣x2+bx+c，直接写出0≤x≤2时y的最大值.
（1）b=-2，c=5，n=6；（2）y的最大值是5． 【解析】试题分析：（1）把（﹣2，0）、（1，2）分别代入﹣x2+bx+c中得到关于b、c的方程组，然后解方程组即可得到b、c的值；然后计算x=﹣1时的代数式的值即可得到n的值； （2）利用表中数据即可求解． 试题解析：（1）根据表格数据可得 ，解得， ∴﹣x2+bx+c=﹣x2﹣2x+5， 当x=﹣1时，﹣x2...
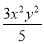的系数是3，次数是4
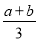不是多项式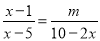
无解，则m＝___________．
