题目内容
3.将一些分数按照某规律排列:$\frac{1}{2}$,$\frac{1}{3}$,$\frac{2}{3}$,$\frac{1}{4}$,$\frac{2}{4}$,$\frac{3}{4}$,$\frac{1}{5}$,$\frac{2}{5}$,$\frac{3}{5}$,$\frac{4}{5}$,…则第2015个数是$\frac{62}{64}$.分析 分母是2的分数有1个,分母是3的分数有2个,分母是4的分数有3个,分母是5的分数有4个,…分母是n的有n-1个,由此得出从2到分母是n的分数共有1+2+3+…+n-1=$\frac{1}{2}$n(n-1)个,由此估算得出2015个数的分母和位置即可.
解答 解:从2到分母是n的分数共有1+2+3+…+n-1=$\frac{1}{2}$n(n-1)个,
∵62×63=3906,63×64=4032,3906<2015×2<4032,
∴第2015个数是的分母是64,分子比64小3,所以第2015个数是$\frac{62}{64}$.
故答案为:$\frac{62}{64}$.
点评 此题考查数字的变化规律,找出数字之间的联系,得出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
12.下面的计算正确的是( )
| A. | 6a-5a=1 | B. | $\sqrt{36}$=±6 | C. | ($\frac{1}{2}$)-1=-2 | D. | 2(a+b)=2a+2b |
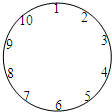 10个人围成一个圆圈做游戏,游戏的规则是:每人心里想好一个数,并把自己想好的数如实地告诉与他相邻的两个人,然后每人将与他相邻两个人的数据的平均数报出来,报出来的数如图所示,则报1的人心里想的数是6.
10个人围成一个圆圈做游戏,游戏的规则是:每人心里想好一个数,并把自己想好的数如实地告诉与他相邻的两个人,然后每人将与他相邻两个人的数据的平均数报出来,报出来的数如图所示,则报1的人心里想的数是6. 如图,直线AB经过点A(-3,0),B(0,2),经过点D(0,4)并且与y轴垂直的直线CD与直线AB交于第一象限内点C.
如图,直线AB经过点A(-3,0),B(0,2),经过点D(0,4)并且与y轴垂直的直线CD与直线AB交于第一象限内点C.