题目内容
5.关于x的分式方程$\frac{m}{x-1}+\frac{3}{1-x}=1$的解为正数(1)用含m的代数式表示该分式方程的解x=m-2;
(2)则m的取值范围是m>2且m≠3.
分析 (1)方程两边乘以x-1化为整式方程得1=-m+2(x-3),用含有m的式子表示出方程的解;
(2)根据分式方程的解为正数,并且分母不为零,可得到满足条件的m的范围.
解答 解:(1)去分母得,m-3=x-1,
解得x=m-2;
(2)∵关于x的分式方程$\frac{m}{x-1}+\frac{3}{1-x}=1$的解为正数,
∴m-2>0,
∴m>2,
∵x-1≠0,
∴x≠1,即m≠3,
故答案为x=m-2;m>2且m≠3.
点评 本题考查了分式方程的解:使分式方程左右两边成立的未知数的值叫分式方程的解,解答本题时,易漏掉m≠3,这是因为忽略了x-1≠0这个隐含的条件而造成的,这应引起同学们的足够重视.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
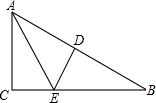 如图,在△ABC中,∠ACB=90°,AE平分∠BAC,DE⊥AB于D,如果AC=3cm,BC=4cm,AB=5cm,那么△EBD的周长为6cm.
如图,在△ABC中,∠ACB=90°,AE平分∠BAC,DE⊥AB于D,如果AC=3cm,BC=4cm,AB=5cm,那么△EBD的周长为6cm.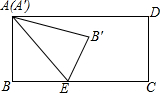 如图,矩形ABCD的边AB=4,BC=7,E为BC上一点,BE=3,连接AE,将矩形ABCD沿AE翻折,翻折后点B与点B′对应,点A与A′对应,再将所得△A′B′E绕着点E旋转,线段A′B′与线段AE交于点P,当PA′=2.4时,△B′AP为等腰三角形.
如图,矩形ABCD的边AB=4,BC=7,E为BC上一点,BE=3,连接AE,将矩形ABCD沿AE翻折,翻折后点B与点B′对应,点A与A′对应,再将所得△A′B′E绕着点E旋转,线段A′B′与线段AE交于点P,当PA′=2.4时,△B′AP为等腰三角形.